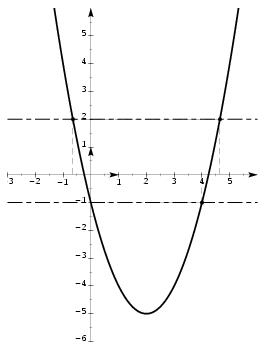
\exo {Une fonction polynome du second degré} On considère la fonction $f$ définie sur $[-10; 10]$ par $$ f (x)= x^2 - 4x -1. $$ On désigne par $C_f$ sa courbe représentative. \let \partie \llappartie \let \partie \centerpartie \partie {A -- Avec une calculatrice} Le plan est rapporté à un repère orthonormal $(O, \vec \imath , \vec \jmath )$. \itemnum \` A l'aide d'une calculatrice, remplir le tableau de valeurs suivant~: $$\vcenter {\offinterlineskip \def \cc#1{% \hbox to 12truemm {\hfill #1\hfill }} \halign { % preamble #\tv && \cc {$#$}& #\tv \cr \noalign {\hrule } & x&& -2&& -1, 5&& -1&& 0&& 0, 5&& 1&& 1, 5&& 2&& 3&& 3,5&& 4& \cr \noalign {\hrule } & f (x)&& && && && && && && && && && && & \cr \noalign {\hrule } }} $$ \itemnum En vous servant du tableau de valeurs, construire la courbe représentative de la fonction $f$. \itemitemalphnum Résoudre graphiquement l'équation $f (x) = 2$. \itemitemalph Résoudre graphiquement l'inéquation $f (x) \leq -1$. \partie {B -- Par le calcul} \itemnum Quelle est l'image par $f$ de $3$~? de $2-2\sqrt 2$~? \itemnum Déterminer les antécédents éventuels de $-1$ par $f$. \itemnum Résoudre l'inéquation $f (x) \leq -1$. \itemnum On voudrait savoir s'il existe des points dont l'ordonnée est $4$. \itemitemalph Quelle équation doit-on résoudre~? \itemitemalph Répondre au problème posé après avoir développé l'expression $(x+1) (x-5)$. \finexo \corrige {} \let \partie \llappartie \partie {A} % \vskip -5mm \itemnum On obtient $$\vcenter {\offinterlineskip \def \cc#1{% \hbox to 12truemm {\hfill #1\hfill }} \halign { % preamble #\tv && \cc {$#$}& #\tv \cr \noalign {\hrule } & x&& -2&& -1, 5&& -1&& 0&& 0, 5&& 1&& 1, 5&& 2&& 3&& 3,5&& 4& \cr \noalign {\hrule } & f (x)&& 11&& 7, 25&& 4&& -1&& -2, 75&& -4&& -4, 75&& -5&& -4&& -2, 75&& -1& \cr \noalign {\hrule } }} $$ \def \epspath {% $HOME/tex_doc/lycee/database/2nd/analyse/fonctions/} \itemnum D'où la courbe~: $$ \superboxepsillustrate {graph_002.ps} $$ \itemalphnum Graphiquement, les solutions de l'équation $f (x) = 2$ correspondent aux abscisses des points d'intersections de la courbe d'équation $y = f (x)$ avec la droite horizontale d'équation $y = 2$. D'où les deux solutions~: \tresultat {$x_1 \approx -0, 6$ et $x_2\approx 4, 6$} . \itemalphnum Graphiquement, les solutions de l'inéquation $f (x) \leq -1$ correspondent aux abscisses des points de la courbe d'équation $y = f (x)$ situés en-dessous de la droite horizontale d'équation $y = -1$. D'où les solutions~: \dresultat {x \in [0;4]} . \partie {B} % \vskip -7mm \itemnum On trouve \dresultat {f (3) = -4} et \dresultat {f (2-2\sqrt 2) = 3}. \itemnum $\bullet $ Dire que le nombre $x$ est un antécédent de $1$ par $f$ revient à dire que $x$ est solution de l'équation $f (x) = 1$. D'où la résolution~: $$ x^2 - 4x - 1 = -1 \qquad \Longleftrightarrow \qquad x^2 - 4x = 0 \qquad \Longleftrightarrow \qquad x (x - 4) = 0 $$ d'où les \tresultat {2~solutions~: $x = 0$ et $x=4$} puisque que l'on a un produit de facteurs égal à zéro. \itemnum Il vient $$ f (x) \leq -1 \quad \Longleftrightarrow \quad x^2 - 4x -1 \leq -1 \quad \Longleftrightarrow \quad x^2 - 4x \leq 0 \quad \Longleftrightarrow \quad x (x - 4) \leq 0 $$ d'où le tableau de signes~: $$\vcenter {\offinterlineskip \eightpoint \rm \halign { % preamble #& \cc {$#$}& \tv #& $#$& \cc {$#$} & \cc {$#$} & \cc {$#$} & \cc {$#$} & \cc {$#$} & $#$ \cr & x && -\infty && 0 && 4 &&+\infty \cr \noalign {\hrule height 1pt} & x-4 &&& + &\tv & + & 0 & - \cr \noalign {\hrule } & x &&& - & 0& + & \tv & + \cr \noalign {\hrule height 1pt} & \rm produit &&& - & 0 & + & 0 & - \cr }}$$ qui permet de conclure~: $f (x) \leq -1 \Longleftrightarrow $ \dresultat {x \in \, ]-\infty ; 0[ \cup ]4; +\infty [}. \itemalphnum Même problème qu'à la question {\bf 2.} L'équation à résoudre est \dresultat {f (x) = 4}. \itemalph Après avoir développé \dresultat {(x+1)(x-5) = x^2 - 4x - 5}, la résolution de l'équation donne~: $$ f (x) = 4 \quad \Longleftrightarrow \quad x^2 - 4x - 1 = 4 \quad \Longleftrightarrow \quad x^2 - 4x -5 = 0 \quad \Longleftrightarrow \quad (x+1) (x - 5) = 0 $$ d'où les \tresultat {2~solutions~: $x = -1$ et $x=5$} puisque que l'on a un produit de facteurs égal à zéro. \fincorrige