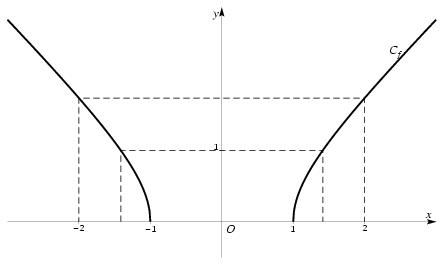
\exo {Lecture du graphe d'une fonction numérique} \catcode`|=12 \input $HOME/tex_doc/format/pstricks/pstricks.tex La courbe $C_f$ ci-dessous est la courbe représentative d'une fonction $f$ définie sur $D = \, ]-\infty ; -1] \cup [1; +\infty [$. \itemnum Observer le graphe de la fonction $f$ puis répondre aux questions suivantes~: \itemitemalph Quel est le signe de $f (x)$ lorsque $x$ est un réel appartenant à $D$~? \itemitemalph Combien vaut $f (1)$~? $f (2)$~? \itemitemalph Quels sont les réels ayant pour image $1$~? \itemnum Résoudre graphiquement l'inéquation $f (x) \leq 1$. \def \epspath {% $HOME/tex_doc/lycee/database/2nd/analyse/fonctions/} %% xsize: 155.89 mm, 443.57 pt %% ysize: 93.13 mm, 265 pt \tmpdimen = 155.89 mm \epsfxsize = .8 \tmpdimen \bgroup \eightpoint \rm $$ \psset{unit=.8pt} \pspicture(-221.78,-43.21)(221.78,221.78) \psset{xunit=71.42,yunit=71.42} \rput(0,1.25){\epsfbox{\epspath lect_005.ps}} \rput(1.414, -.1){$\sqrt 2 $} \rput(-1.414, -.1){$-\sqrt 2$} \rput(-.15, 1.9){$\sqrt 3$} \endpspicture $$ \egroup \itemnum Soit $a$ un réel positif vérifiant $a\leq 2$. On considère l'équation $f (x) = a$. \item {} Utiliser le graphique pour expliquer pourquoi une telle équation a toujours 2~solutions. \finexo \corrige \itemalphnum Apparemment, $f (x)$ est \tresultat {toujours positif pour $x\in D$}. \itemalph On lit sur le graphique \dresultat {f (1) = 0} et $\dresultat {f (2) = 3}$. \itemalph On lit deux réels ayant $1$ pour image~: \tresultat {$\sqrt 2$ et $-\sqrt 2$}. \itemnum On a $f (x) \leq 1$ si et seulement si \dresultat {x \in [-\sqrt 2; -1] \cup [1; \sqrt 2]} \itemnum Considérons la droite horizontale d'équation $y = a$ avec $0\leq a \leq 2$. Il est clair que, quelle que soit la valeur de $a$, cette droite possède deux points d'intersection avec la courbe $C_f$. Or les solutions de l'équation $f (x) = a$ correspondent aux abscisses des points d'intersection de la droite $y=a$ avec la courbe $y=f (x)$. On en conclut que \tresultat {l'équation $f (x) = a$ admet toujours 2~solutions} si $0\leq a\leq 2$. \fincorrige