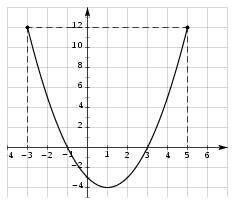
\exo {Images et antécédents, lecture de graphique} \let \partie \centerpartie On vous a représenté ci-dessous la courbe représentative d'une fonction $f$. \def \epspath {% $HOME/tex_doc/lycee/database/2nd/analyse/fonctions/} $$ \superboxepsillustrate {lect_009.ps} $$ \partie {A : Lecture graphique} \itemnum Lire sur le graphique l'ensemble de définition de $f$. \itemnum Déterminer graphiquement les solutions de l'inéquation $f (x)>0$. \itemnum Déterminer graphiquement l'image de $2$ par $f$. \itemnum Déterminer graphiquement les antécédents de $-3$ par $f$. \partie {B : Par le calcul} On admet maintenant que la fonction $f$ est définie par~: \qquad $f (x) = (x - 1)^2 - 4$. \itemitemalphnum Montrer que l'expression factorisée de $f (x)$ est $$ f (x) = (x+1) (x-3) $$ \itemitemalph Déterminer l'expression développée de $f (x)$. \itemnum Déterminer les images par $f$ des nombres suivant~: $$ \alph \quad -{1\over 4} \qquad \qquad \alph \quad \sqrt 2 \qquad \qquad \alph \quad 1 + \sqrt 3 $$ \itemnum Résoudre l'équation $f (x) = 0$. %%\itemnum Déterminer les antécédents éventuels de $-3$ par $f$. \finexo \corrige \let \partie \llappartie \partie {A} \vskip -5mm \itemnum On voit sur le graphique que la courbe de $f$ n'existe que pour les réels $x$ entre $-3$ et $5$. D'où l'ensemble de définition de $f$~: \dresultat {{\cal D} = [-3; 5]}. \itemnum Graphiquement, on lit que $f (x)$ est strictement positive si et seulement si \dresultat {x \in [-3; -1[ \, \cup \, ]3; 5]}. \itemnum On lit sur le graphique~: \dresultat {f (2) \approx -3}. \itemnum Toujours graphiquement, on trouve \tresultat {2~antécédents pour $-3$~: $0$ et 2}. \partie {B} \vskip -5mm \itemitemalphnum On reconnaît une identité remarquable dans l'écriture proposée pour $f (x)$. Il vient alors $$\eqalign { f (x) &= (x-1)^2 - 4 = (x-1)^2 - 2^2 \cr &= (x-1-2) (x-1+2) \qquad {\rm soit} \qquad \dresultat {f (x) = (x-3)(x+1)}. \cr }$$ \itemalph Quant à l'écriture développée, on obtient facilement \dresultat {f (x) = x^2 - 2x -3}. \itemnum Pour les images demandées, et en utilisant l'écriture $f (x) = (x-1)^2 -4$, il vient $$\displaylines { \bullet \quad f \left( - {1\over 4}\right) = \left( - {5\over 4}\right) ^2 - 4 = {25\over 16} - {4\times 16\over 16} \qquad {\rm soit} \qquad \dresultat {f \left( - {1\over 4}\right) = -{39\over 16}} \cr \bullet \quad f (\sqrt 2) = (\sqrt 2 -1)^2 - 4 = 2 + 1 - 2\sqrt 2 - 4 \qquad {\rm soit} \qquad \dresultat {f (\sqrt 2) = -1 - 2\sqrt 2} \cr \bullet \quad f (1+ \sqrt 3) = (\sqrt 3)^2 - 4 \qquad {\rm soit} \qquad \dresultat {f (1+\sqrt 3) = -1} \cr }$$ \itemnum En prenant l'écriture factorisée pour $f$, l'équation proposée se résoud immédiatement puisque l'on a un produit de facteurs égal à 0. D'où $$ f (x) = 0 \quad \Longleftrightarrow \quad (x-3) (x+1) = 0 \quad \Longleftrightarrow \quad \dresultat {x \in \{ 3; -1\}}. $$ %% \itemnum Il s'agit de résoudre l'équation $f (x) = -3$. En utilisant %% l'expression développée de $f (x)$, il vient %% $$ %% x^2 -2x - 3 = -3 %% \quad \Longleftrightarrow \quad %% x^2 - 2 x = 0 %% \quad \Longleftrightarrow \quad %% x (x - 2) = 0 %% $$ %% Comme on a un produit de facteurs égal à $0$, on obtient immédiatement %% les deux solutions. D'où l'ensemble des solutions~: \dresultat {{\cal %% S} = \{0; 2\}}. \fincorrige