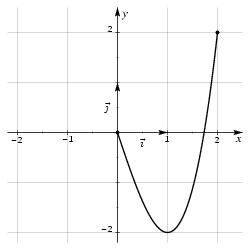
\exo {Une fonction impaire à déterminer} Soit $g$ la fonction définie sur l'intervalle $[-2 ; 2]$. On sait que $g$ est impaire, et on a ci-dessous le tracé de la courbe $C_g$ d'équation $y = g (x)$ pour $x\in [0; 2]$~: \def \epspath {% $HOME/tex_doc/lycee/database/2nd/analyse/fonctions/} $$ \superboxepsillustrate {parite_003.ps} $$ \itemnum Compléter le tracé ci-dessus pour $x \in [-2; 0]$. \itemnum Donner le tableau de variation de la fonction $g$ pour $x \in [-2; 2]$ (lecture graphique). \itemnum On propose comme fonction $g$~: $$ \alph \quad g (x) = x^3 - 3x + 3 \qquad \qquad \alph \quad g (x) = x^3 - 3x. $$ Laquelle choissisez-vous~? Pourquoi~? \itemitemalphnum Résoudre dans $\rset $~: $x^3 - 3x = 0$. \itemitemalph Résoudre dans $\rset $~: $x^3 - 3x \leq 0$. \itemnum Quels sont les antécédents de $0$ par la fonction $g$~? \finexo \corrige \itemnum \def \epspath {% $HOME/tex_doc/lycee/database/2nd/analyse/fonctions/} $$ \superboxepsillustrate {parite_003a.ps} $$ \itemnum On lit~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -2 && -1&& 1&& 2 \cr \noalign {\hrule height 1pt} \buucenter {$f (x)$}&& \down {$-2$}& \brightuuparrow & \buup {$2$}& \brightddownarrow & \down {$-2$}& \brightuuparrow & \buup {$2$} \cr }} }$$ \itemnum Des 2~fonctions proposées, c'est \dresultat {g (x) = x^3 - 3x} qu'il faut choisir~: c'est la seule des 2~fonctions qui soit impaire, et c'est la seule dont la courbe représentative passe par l'origine $O (0, 0)$ (autrement dit, c'est la seule à vérifier $g (0) = 0$). \itemalphnum Il vient $$ x^3 - 3x = 0 \quad \Longleftrightarrow \quad x (x^2 - 3) = 0 \quad \Longleftrightarrow \quad x (x - \sqrt 3) (x + \sqrt 3)= 0 $$ On a un produit de 3~facteurs égal à zéro, donc l'un des facteurs est nul. D'où l'ensemble des solutions~: \dresultat {{\cal S} = \{-\sqrt 3; 0; \sqrt 3\}}. \itemalph De la même façon que précédemment, il vient~: $$ x^3 - 3x \leq 0 \quad \Longleftrightarrow \quad x (x^2 - 3) \leq 0 \quad \Longleftrightarrow \quad x (x - \sqrt 3) (x + \sqrt 3)\leq 0 $$ Un tableau de signes permet alors de conclure~: $$\vcenter {\offinterlineskip \eightpoint \rm \halign { % preamble \tv #& \cc {$#$}& \tv #& $#$& \cc {$#$} & \cc {$#$} & \cc {$#$} & \cc {$#$} & \cc {$#$} & \cc {$#$} & \cc {$#$} & $#$ \cr & x && -\infty && -\sqrt 3 && 0&& \sqrt 3 &&+\infty \cr \noalign {\hrule height 1pt} & x &&& - & \tv & - & 0 & + & \tv & + & \cr \noalign {\hrule } & x-\sqrt 3 &&& - & \tv & - & \tv & - & 0 & + \cr \noalign {\hrule } & x+\sqrt 3 &&& - & 0 & + & \tv & + & \tv & + \cr \noalign {\hrule height 1pt} & \rm produit &&& - & 0 & + & 0 & - & 0 & + \cr \noalign {\hrule } }}$$ D'où l'ensemble des solutions~: \dresultat {{\cal S} = ]-\infty ; -\sqrt 3] \cup [0 ; \sqrt 3]}. \itemnum Chercher les antécédents de $0$ par $g$ revient à résoudre l'équation $g (x) = 0$. La question {\bf 4.}{\sl a\/}) permet alors de répondre immédiatement~: \tresultat {$0$ possède $3$~antécédents par $g$~: $-\sqrt 3$, $0$ et $\sqrt 3$}. \fincorrige