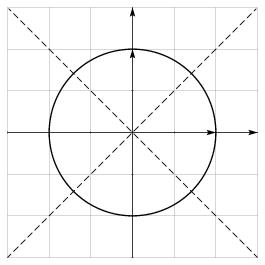
\exo {Cercle trigonométrique, équations} Dans le plan muni d'un repère orthonormé, on a représenté ci-dessous le cercle trigonométrique. \def \epspath {% $HOME/tex_doc/lycee/database/2nd/analyse/trigo/} $$ \superboxepsillustrate {synt_001.ps} $$ \itemitemalphnum Placer sur le graphique ci-dessus les points correspondant aux nombres $$ 0, \qquad {\pi \over 2}, \qquad {\pi \over 4}, \qquad {\pi \over 3}, \qquad {3\pi \over 4}, \qquad {9\pi \over 4}, \qquad {2\pi \over 3}, \qquad -{5\pi \over 2}, $$ \itemitemalph En déduire les valeurs exactes de $$ \cos \left( {2\pi \over 3}\right) \qquad {\rm et} \qquad \sin \left( {2\pi \over 3}\right) $$ \itemitemalphnum \` A l'aide du cercle ci-dessus, résoudre dans l'intervalle $[-\pi ; \pi ]$ l'équation $$ \cos x = {1\over 2}. \leqno (E) $$ \itemitemalph Toujours à l'aide du graphique, résoudre l'équation $(E)$ sur l'intervalle $[0; 2\pi ]$. \itemnum \` A l'aide du cercle ci-dessus, résoudre dans l'intervalle $[-\pi ;\pi ]$ l'équation $$ \sin x = {1\over 2}. \leqno (E') $$ \itemnum Soit $x$ un nombre de l'intervalle $[0;\pi ]$ dont le cosinus vaut $-4/5$. Déterminer $\sin x$. \finexo \corrige {} \itemalphnum \def \epspath {% $HOME/tex_doc/lycee/database/2nd/analyse/trigo/} $$ \superboxepsillustrate {synt_001b.ps} $$ \itemalph Vu les symétries du cercle, et connaissant les cosinus et sinus de $\pi /3$, on en déduit aisément $$ \dresultat {\cos \left( {2\pi \over 3}\right) = -{1\over 2}} \qquad {\rm et} \qquad \dresultat {\sin \left( {2\pi \over 3}\right) = {\sqrt 3\over 2}}. $$ \itemalphnum \alph \ \def \epspath {% $HOME/tex_doc/lycee/database/2nd/analyse/trigo/} $$ \epsfxsize = .4\hsize \superboxepsillustrate {synt_001c.ps} \qquad \qquad \epsfxsize = .4\hsize \superboxepsillustrate {synt_001d.ps} $$ On lit sur le cercle trigonométrique les solutions de nos deux équations. On trouve ainsi $$ \tresultat {2~solutions sur $[-\pi ;\pi ])$~: $\pi /3$ et $-\pi /3$}, \qquad {\rm et} \qquad \tresultat {2~solutions sur $[0; 2\pi ]$~: $\pi /3$ et $5\pi /3$}. $$ \itemnum De la même façon, on trouve les 2~solutions sur $[-\pi ; \pi ]$ de l'équation $\sin x = 1/2$~: \tresultat {$\pi /6$ et $5\pi /6$} . $$ \epsfxsize = .4\hsize \superboxepsillustrate {synt_001e.ps} $$ \itemnum On connaît le cosinus du nombre $x$ et on cherche son sinus. Sachant que l'on a toujours $\sin ^2 x + \cos ^2 x = 1$, il vient facilement $$ \sin ^2 x = 1 - \cos ^2 x = 1 - \left( - {4\over 5} \right) ^2 = 1 - {16\over 25} \qquad {\rm soit} \qquad \sin ^2 x = {9\over 25}. $$ \` A ce stade, on a donc 2~possibilités~: soit $\displaystyle { \sin x = \sqrt {9\over 25} = {3\over 5} }$, soit $\displaystyle { \sin x = - \sqrt {9\over 25} = -{3\over 5} }$. Mais comme l'on sait que $x\in [0; \pi ]$, on en déduit que son sinus est positif. La seule solution possible est donc \dresultat {\sin x = {3\over 5}}. \fincorrige