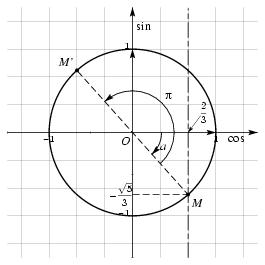
\exo {Un point du cercle trigonométrique} Soit $a$ un nombre réel vérifiant $$ \cos a = {2\over 3} \qquad {\rm et} \qquad -{\pi \over 2} < a <0. $$ \itemnum Placer sur le cercle trigonométrique le point $M$ qui correspond à l'angle $a$. \itemnum Calculer la valeur exacte de $\sin a$. \itemnum Placer le point $M'$ du cercle trigonométrique qui correspond à l'angle $a+\pi $. En déduire les coordonnées de $M'$. \finexo \corrige \def \epspath {% $HOME/tex_doc/lycee/database/2nd/analyse/trigo/} \itemnum $$ \superboxepsillustrate {synt_002.ps} $$ \itemnum On sait que l'on a toujours $\cos ^2 x + \sin ^2 x = 1$. Utilisée en $x=a$, et connaissant $\cos a$, cette relation nous donne $$ \sin ^2 a = 1 - \left( {2\over 3}\right) ^2 = 1 - {4\over 9} = {5\over 9} \qquad {\rm d'où} \qquad \sin a = \sqrt {5\over 9} \quad {\rm ou} \quad \sin a = -\sqrt {5\over 9} $$ Sachant maintenant que $a \in \, ]-\pi /2; 0[$, on en déduit que $\sin a$ est négatif. Ce qui permet de conclure~: $$ \dresultat {\sin a = -{\sqrt 5\over 3}}. $$ \itemnum Par symétrie, on en déduit que les coordonnées de $M'$ sont \dresultat {M' \left( -{2\over 3}; {\sqrt 5\over 3}\right) }. \fincorrige