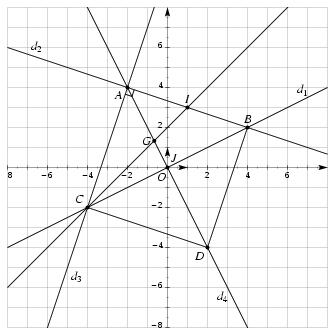
\exo {Droites : un exercice de synthèse} \let \partie \centerpartie Le plan est rapporté à un repère orthonormé $(O, \vec \imath , \vec \jmath )$ d'unité graphique 1~cm (ou 1~grand carreau). \partie {A} On donne les points $A (-2; 4)$, $B (4; 2)$ et $C (-4; -2)$. \itemnum Placer les points $A$, $B$ et $C$. \itemnum Calculer les coordonnées des vecteurs $\overrightarrow {AB}$, $\overrightarrow {AC}$, $\overrightarrow {BC}$. \itemnum Calculer les longueurs $AB$, $AC$ et $BC$. \itemnum Que peut-on dire du triangle $ABC$~? \itemnum Calculer l'aire du triangle $ABC$. \partie {B} \itemnum Soit $(d_1)$ la droite d'équation~: \qquad $x-2y = 0$. \itemitemalph Quel est le coefficient directeur de $(d_1)$~? \itemitemalph Donner un vecteur directeur de $(d_1)$. \itemitemalph Construire $(d_1)$ sur la figure précédente. \itemnum Soit $(d_2)$ la droite d'équation~: \qquad $\displaystyle { y = - {1\over 3} x + {10\over 3} }$. \itemitemalph Quel est le coefficient directeur de $(d_2)$~? \itemitemalph Construire $(d_2)$ sur la figure précédente. \itemitemalph Les droites $(d_1)$ et $(d_2)$ ont-elles un point commun~? Préciser. \itemitemalphnum \' Etablir une équation cartésienne de la droite $(d_3)$ passant par $A$ et $C$. \itemitemalph En déduire une équation réduite. \itemitemalph Dire pourquoi les droite $(d_2)$ et $(d_3)$ sont perpendiculaires. \itemitemalph Retrouver le résultat de la question {\bf 4.}, partie {\bf A}. \partie {C} \itemnum Déterminer une équation de la droite $(OA)$, notée $(d_4)$. \itemnum Pourquoi $(d_4)$ est-elle perpendiculaire à $(d_1)$~? \itemnum Soit $D (2; -4)$. Prouver que $D \in (d_4)$. \itemnum Quelle est la nature du quadrilatère $ABDC$~? Donner son aire. \partie {D} \itemnum Déterminer les coordonnées de $I$ et $J$, les milieux respectifs des segments $[AB]$ et $[BC]$. \itemnum Déterminer une équation de $(AJ)$ et une équation de $(CI)$. \itemnum En déduire les coordonnées du centre de gravité du triangle $ABC$. \finexo \corrige \let \partie \llappartie \partie {A} % \vskip -5mm % \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/analytique/} \itemnum $$ \superboxepsillustrate {synt_004.ps} $$ \itemnum En utilisant les formules du cours, il vient $$ \overrightarrow {AB} {4 - (-2)\choose 2 -4} \quad {\rm soit} \quad \dresultat {\overrightarrow {AB} {6\choose -2}} \quad \hbox {puis, de la même façon} \quad \dresultat {\overrightarrow {AC} {-2\choose -6}} \qquad {\rm et} \qquad \dresultat {\overrightarrow {BC} {-8\choose -4}} $$ \itemnum En utilisant les calculs précédents, on trouve $$ AB = \sqrt {6^2 + (-2)^2} \quad {\rm soit} \quad \dresultat {AB = \sqrt {40} = 2\sqrt {10}} $$ puis, de la même façon $$ \dresultat {AC = \sqrt {40} = 2\sqrt {10}} \qquad {\rm et} \qquad \dresultat {AB = \sqrt {80} = 4\sqrt {5}} $$ \itemnum Au vu des calculs précédents, on peut donc affirmer que \tresultat {$ABC$ est isocèle rectangle en $A$}. \itemnum Son aire est donnée par le calcul $$ {\cal A} (ABC) = {1\over 2} AB \times AC \qquad {\rm soit} \qquad \dresultat {{\cal A} (ABC) = 20\cm ^2} $$ puisque l'unité d'aire est de $1\cm ^2$. \partie {B} % \vskip -8mm \itemalphnum L'équation réduite de la droite $(d_1)$ est $\displaystyle { (d_1)~: y = {1\over 2} x }$, d'où le \tresultat {coefficient directeur de $(d_1)$~: $\displaystyle {1\over 2}$}. \itemalph Un vecteur directeur de $(d_1)$ est donc \dresultat {\vec u {1\choose 1/2}}, et $\displaystyle { \vec v {2\choose 1} = 2\vec u }$ en est un autre. \itemalphnum Le \tresultat {coefficient directeur de $(d_2)$ est $\displaystyle -{1\over 3}$}. \advance \alphno by 1 \itemalph Les droite $(d_1)$ et $(d_2)$ n'ont ps le même coefficient directeur, donc elles sont sécantes, et on peut affirmer qu'\tresultat {elles ont un point en commun}. En regardant le dessin, on a l'impression que le point $B$ est ce point commun. Il ne reste plus qu'à vérifier que les coordonnées de $B$ vérifient les équations de $(d_1)$ et de $(d_2)$ pour prouver que \dresultat {(d_1) \cap (d_2) = \{ B\} }. \itemalphnum Un point $M (x, y)$ appartient à la droite $(AC)$ si et seulement si $$\eqalign { \overrightarrow {AM} \quad {\rm et} \quad \overrightarrow {AC} \quad {\rm colinéaires} \qquad &\Longleftrightarrow \qquad {x+2\choose y-4} \quad {\rm et} \quad {-2\choose -6} \quad {\rm colinéaires} \cr &\Longleftrightarrow \qquad -6 (x+2) + 2 (y-4) = 0 \cr &\Longleftrightarrow \qquad -6 x -12 + 2y -8 = 0 \cr }$$ d'où une équation cartésienne de $(AC)~: $\dresultat {(d_3)~: -6x+2y-20=0}. \itemalph L'équation réduite de $(AC)$ est donc \dresultat {y = 3x+10}. \itemalph Le coefficient directeur de $(d_3)$ est $3$ et le coeeficient directeur de $(d_2)$ est $-1/3$. Le produit de ces coefficients directeurs est égal à $-1$, ce qui prouve que les droites \tresultat {$(d_2)$ et $(d_3)$ sont perpendiculaires}. \itemalph Les points $A$ et $C$ sont sur $(d_3)$ par définition de $(d_3)$, et on a vu dans la question {\bf B-2.}{\sl c\/}) que le point $B$ était sur la droite $(d_2)$. Reste à vérifier que le point $A$ est bien sur la droite $(d_2)$ pour retrouver le fait que \tresultat {$ABC$ est rectangle en $A$}. \partie {C} %% \vskip -5mm \itemnum La droite $(d_4)$ d'équation $y = mx+p$ passe par les points $O (0, 0)$ et $A (-2, 4)$, d'où le système d'équation $$ \cases { 0 = m \times 0 + p \cr 4 = m \times (-2) + p \cr } \quad \Longleftrightarrow \quad \cases { 0 = p \cr -2 = m \cr } \qquad {\rm d'où} \qquad \dresultat {(d_4)~: y = -2x}. $$ \itemnum Le coefficient directeur de $(d_4)$ est $-2$ alors que celui de $(d_1)$ est $1/2$ (d'après {\bf A-1.}{\sl a\/})). Le produit de ces coefficients directeurs est égal à $-1$, ce qui prouve que \tresultat {$(d_1)$ et $(d_4)$ sont perpendiculaires}. \itemnum Les coordonnées $(2;-4)$ de $D$ vérifient l'équation $y = -2x$ de $(d_4)$, donc \tresultat {$D$ appartient à $(d_4)$}. \itemnum Les coordonnées du vecteur $\overrightarrow {CD}$ sont $$ \overrightarrow {CD} {2+4\choose -4+2} \qquad {\rm soit} \qquad \overrightarrow {CD} {6\choose -2} = \overrightarrow {AB} \quad \hbox {d'après {\bf A-1.}} $$ donc $ABDC$ est un parallélogramme, or il possède un angle droit en $A$ (d'après {\bf A-4.}), donc \tresultat {$ABDC$ est un carré}. \item {} Son aire est donnée par le calcul ${\cal A} (ABDC) = AB\times AC$ soit \dresultat {{\cal A} (ABDC) = 40\cm ^2}. \partie {D} %% \vskip -5mm %% \itemnum Il vient $$ I \left( {1\over 2} (-2+4); {1\over 2} (4+2) \right) \quad {\rm soit} \quad \dresultat {I (1;3)} \qquad \hbox {et, de la même façon} \qquad \dresultat {J (0;0)} $$ \itemnum Comme les points $J$ et $O$ sont confondus, on a déjà \dresultat {$(AJ)~: y = -2x$} puisque $(AJ)$ et $(d_4)$ sont confondues. \item {} Pour $(CI)$, on peut utiliser le fait que le point $M (x, y)$ est sur $(CI)$ si et seulement si $$\eqalign { \overrightarrow {CM} \quad {\rm et} \quad \overrightarrow {CI} \quad {\rm colinéaires} \qquad &\Longleftrightarrow \qquad {x+4\choose y+2} \quad {\rm et} \quad {5\choose 5} \quad {\rm colinéaires} \cr &\Longleftrightarrow \qquad 5 (x+4) - 5 (y+2) = 0 \cr &\Longleftrightarrow \qquad 5x+20 - 5y-10 = 0 \cr }$$ d'où une équation cartésienne de $(CI)~: $\dresultat {(CI)~: x-y+2=0}. \itemnum Les droite $(AJ)$ et $(CI)$ sont des médianes du triangle $ABC$. Le centre de gravité du triangle $ABC$ est situé à l'intersection de ces médianes. Chercher les coordonnées de $G$ revient donc à résoudre le système $$ \cases { y = -2x \cr x-y+2 = 0 \cr } \quad \Longleftrightarrow \quad \cases { y = -2x \cr x+2 = -2x \cr } \quad \Longleftrightarrow \quad \cases { y = 4/3 \cr x = -2/3 \cr } $$ d'où les coordonnées du point cherché~: \dresultat {G \left( -{2\over 3}; {4\over 3}\right) }. \fincorrige