synt_005.tex

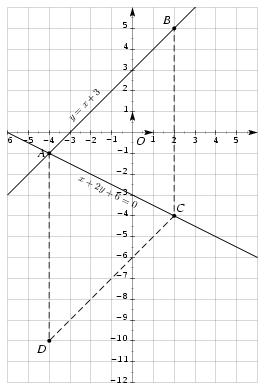
\exo {Des pointset des droites\dots}
 
Le plan est muni d'un repère orthonormal. $A$, $B$ et $C$ sont trois
points du plan. On sait que les droites $(AB)$ et $(AC)$ ont
respectivement pour équation~:
$$
   (AB)~: \quad y = x + 3
      \qquad {\rm et} \qquad
   (AC)~: \quad x + 2y + 6 = 0.
$$
 
\itemnum Tracer ces deux droites et calculer les coordonnées de $A$.
 
\itemnum Calculer les coordonnées des points $B$ et $C$ sachant que
      leurs ordonnées respectives sont $5$ et $-4$.
 
\itemnum Trouver, par la méthode de votre choix, une équation de la
droite $(BC)$.
 
\itemnum Calculer les coordonnées du point $D$ tel que $BCDA$ soit un
parallélogramme. 
 
\finexo
 
\corrige
 
\def \epspath {%
   $HOME/tex_doc/lycee/database/2nd/geometrie/analytique/}
\itemnum 
$$
   \superboxepsillustrate {synt_005.ps}
$$
Rechercher l'intersection des deux droites $(AB)$ et $(AC)$ revient à
résoudre le système
$$
   \cases {
      y = x+3
   \cr
      x+2y+6 = 0
   \cr }
      \quad \Longleftrightarrow \quad
   \cases {
      y = x+3
   \cr
      x+2(x+3)+6 = 0
   \cr }
      \quad \Longleftrightarrow \quad
   \cases {
      y = x+3
   \cr
      x = -4
   \cr }
$$
d'où les coordonnées du point cherché~: \dresultat {A (-4; -1)}.
 
\itemnum La condition \og $B$ est le point de $(AB)$ d'ordonnée $5$\fg
\ se traduit par le système
$$
   \cases {
      y = x+3
   \cr 
      y = 5
   \cr }
      \quad {\rm d'où} \quad
   \tresultat {les coordonnées cherchées~: $B (2; 5)$}
$$
De la même façon, la condition \og \sl $C$ est le point de $(AC)$ d'ordonnée $-4$\fg
\ se traduit par le système
$$
   \cases {
      x+2y+6=0
   \cr 
      y = -4
   \cr }
      \quad {\rm d'où} \quad
   \tresultat {les coordonnées cherchées~: $C (2; -4)$}
$$
 
\itemnum Il est immédiat que les abscisses des points $B$ et $C$ sont
      identiques égaux à $2$. La droite $(BC)$ est donc parallèle à
      l'axe des ordonnées et son équation est \dresultat {(BC)~: x = 2}.
 
\itemnum Notons $(x; y)$ les coordonnées du point $D$. Le quadrilatère
      $BCDA$ est un parallèlogramme si et seulement si
      $\overrightarrow {C} = \overrightarrow {AD}$, d'où le système
      d'équations
$$
   {2 - 2\choose -4 - 5} = {x + 4\choose y + 1}
     \quad \Longleftrightarrow \quad
   \cases {
      x + 4 = 0
   \cr
      y + 1 = -9
   \cr }
      \qquad {\rm d'où} \qquad
   \dresultat {D (-4; -8)}.
$$
 
\fincorrige