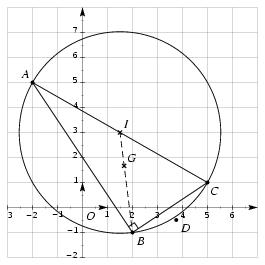
\exo {Triangle rectangle et cercle circonscrit} \itemnum Dans le plan muni d'un repère orthonormal $(O, \vec \imath , \vec \jmath )$ (unité graphique~: 1~cm), placer les points $$ A (-2; 5) \qquad \qquad B (2; -1) \qquad \qquad C(5; 1). $$ \itemnum Démontrer que le triangle $ABC$ est rectangle. \itemnum Calculer les coordonnées du milieu $I$ de $[AC]$, puis celles de $G$, le centre de gravité du triangle $ABC$. \itemnum Déterminer, en $\cm ^2$, et à $10^{-1}$ près, l'aire $\cal A$ de du cercle circonscrit au triangle $ABC$. \finexo \corrige \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/analytique/} \itemnum $$ \superboxepsillustrate {synt_006.ps} $$ \itemnum Un rapide calcul de distances nous donne $$ AB = \sqrt {4^2 + (-6)^2} = \sqrt {52}, \qquad \qquad BC = \sqrt {3^2 + 2^2} = \sqrt {13} \qquad {\rm et}\qquad AC = \sqrt {7^2 + (-4)^2} = \sqrt {65} $$ La relation de Pythagore nous prouve alors que \tresultat {$ABC$ rectangle en $B$}. \itemnum Il vient immédiatement $$ (x_I; y_I) = \left( {-2+5\over 2}; {5+1\over 2}\right) \qquad {\rm soit}\qquad \dresultat {I \left( {3\over 2}; 3\right)} $$ Quand au centre de gravité $G$, on sait qu'il est situé aux deux-tiers de chacune de médiane. En particulier, on aura $$ \overrightarrow {BG} = {2\over 3} \overrightarrow {BI} $$ En notant $(x; y)$ les coordonnées du point $G$, on a donc à résoudre le système $$ {x-2\choose y+1} = {2\over 3} {3/2 - 2\choose 3+1} \quad \Longleftrightarrow \quad \cases { x-2 = -1/3 \cr y+1 = 8/3 \cr } \quad \Longleftrightarrow \quad \cases { x = 5/3 \cr y = 5/3 \cr } $$ D'où le point cherché \dresultat {G \left( {5\over 3}; {5\over 3} \right)}. \itemnum Dans un triangle rectangle, le cercle circonscrit a pour centre le milieu de l'hypothénuse. Ici le centre de notre cercle est donc $I$, et son rayon est ${1\over 2}AC = \sqrt {65}/2$. La surface étant donnée par la formule $S = \pi r^2$, la surface de notre cercle est $$ \dresultat {S = {65\pi \over 4}\cm ^2 \approx 51, 05\cm ^2} $$ \fincorrige