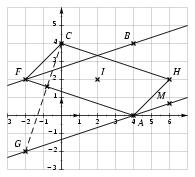
\exo {Petit problème de géométrie analytique} Dans le plan muni d'un repère orthonormé $(O, \vec \imath , \vec \jmath \,)$, on considère les points $$ A (4; 0), \qquad \qquad B (4; 4) \qquad \qquad C (0; 4) \qquad \qquad F (-2; 2) \qquad \qquad G (-2; -2). $$ \itemnum Faire une figure que l'on complètera au fur et à mesure. \itemitemalphnum Tracer sur la figure précédente les droites $d_1$ et $d_2$ d'équations respectives~: $$ d_1~: y = -x + 4 \qquad {\rm et} \qquad d_2~: y = 2. $$ \itemitemalph Quel est le coefficient directeur de $d_1$, de $d_2$? \itemitemalph Déterminer par le calcul les coordonnées du point d'intersection de $d_1$ et $d_2$. \itemitemalphnum Déterminer les coordonnées du point $H$ tel que $AFCH$ soit un parallélogramme. \itemitemalph Déterminer les coordonnées du centre $I$ de ce parallélogramme. \itemitemalphnum Déterminer les coordonnées des vecteurs $\overrightarrow {AG}$ et $\overrightarrow {BF}$. \itemitemalph Les droites $(AG)$ et $(BF)$ sont-elles parallèles~? (Justifier.) \itemitemalph Que peut-on dire du quadrilatère $ABFG$~? (Justifier.) \itemitemalph Soit $M$ un point de coordonnées $(6; y)$. Déterminer son ordonnée $y$ pour que les droites $(AM)$ et $(FB)$ soient parallèles. \itemitemalphnum Déterminer une équation de la droite $(CG)$. \itemitemalph Déterminer, par le calcul, une équation de la droite $(AF)$. \itemitemalphnum Résoudre le système de 2~équations à 2~inconnues~: $$ \cases { y = 3x + 4 \cr y = -{1\over 3} x + {4\over 3} \cr } $$ \itemitemalph Interprétation géométrique de ce calcul~? \itemnum Déterminer une équation de la parallèle à $(AF)$ passant par $C$. \finexo \corrige \itemnum \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/analytique/} $$ \superboxepsillustrate {synt_007.ps} $$ \itemalphnum \alph \quad Le \tresultat {coefficient directeur de $d_1$ est $-1$}, alors que le \tresultat {coefficient directeur de $d_2$ est $0$} \itemalph Déterminer les coordonnées du point d'intersection revient à résoudre le système~: $$ \cases { y = -x+4 \cr y = 2 \cr } \quad \Longrightarrow \quad \cases { 2 = -x+4 \cr y = 2 \cr } \quad \Longrightarrow \quad \cases { x = 2 \cr y = 2 \cr } $$ d'où \tresultat {l'unique point d'intersection~: $(2, 2)$}. \itemalphnum Le quadrilatère $AFCH$ est un parallélogramme si et seulement si $\overrightarrow {AH} = \overrightarrow {FC}$. Posons $H (x, y)$. Il vient alors le calcul $$ \overrightarrow {AH} = \overrightarrow {FC} \quad \Longleftrightarrow \quad {x - 4\choose y} = {2\choose 2} \quad \Longleftrightarrow \quad \cases { x - 4 = 2 \cr y = 2 \cr} \qquad {\rm d'où} \qquad \dresultat {H (6; 2)} $$ \itemalph Le point $I$ est le milieu de la diagonale $[AC]$. D'où le calcul $ I \left( {4 + 0\over 2}; {0 + 4\over 2} \right) $, soit \dresultat {I (2; 2)}. \itemalphnum Il vient~: $$ \overrightarrow {AG} = {-6 \choose -2} \qquad {\rm et} \qquad \overrightarrow {BF} = {-6 \choose -2} $$ \itemalph Ces 2~vecteurs étant égaux, il sont en particulier colinéaires. On en déduit que~: $$ \tresultat {les droites $(AG)$ et $(BF)$ sont parallèles}. $$ \itemalph Au vu de la question précédente, il est clair que $M$ est un point de la droite $(AG)$. Or cette droite est de coefficient directeur $-2/-6 = 1/3$ (d'après la question précédente) et elle passe par le point $A (4; 0)$. On en déduit que son équation réduite est de la forme $$ y = {1\over 3} x + b \qquad {\rm avec} \qquad 0 = {1\over 3} \times 4 + b \qquad \hbox {d'où l'équation} \qquad (AG)~: y = {1\over 3} x - {4\over 3}. $$ Notre point $M$ étant le point d'abscisse $6$ de cette droite, on a alors facilement \dresultat {M \left( 6 ; {2/3}\right) }. {\bf rque~:} on aurait également pu utiliser la relation de colinéarité des vecteurs $\overrightarrow {AM}$ et $\overrightarrow {FB}$. \itemalphnum L'équation réduite de $(AF)$ est de la forme $y = ax+b$. Or $$ \overrightarrow {AF} {-6\choose 2} \qquad {\rm donc} \qquad a = {2\over -6} = -{1\over 3}. $$ De plus, $A$ est sur cette droite, d'où $$ 0 = -{1\over 3} \times 4 + b \qquad {\rm et} \qquad b = {4\over 3}. \qquad \hbox {Finalement, on obtient} \qquad \dresultat {(AF)~: y = -{1\over 3} x + {4\over 3}} $$ \itemalph En procédant comme précédemment, on trouve \dresultat {(CG)~: y = 3x + 4}. \itemnum Résoudre le système donné revient à chercher l'intersection des droites $(AF)$ et $(CG)$. Il vient~: $$ \cases { y = 3x + 4 \cr y = -{1\over 3} x + {4\over 3} \cr } \quad \Longleftrightarrow \quad \cases { y = 3x + 4 \cr 3y = -x + 4 \cr } \quad \Longleftrightarrow \quad \cases { y = 3x + 4 \cr 3(3x+4) = -x + 4 \cr } \quad \Longleftrightarrow \quad \cases { y = 8/5 \cr x = -4/5 \cr } $$ d'où \tresultat {le point d'intersection de $(AF)$ et $(CG)$~: $\displaystyle {\left( - {4\over 5}; {8\over 5}\right)}$} \itemnum Une parallèle à (AF) possède le même cefficient directeur que $(AF)$. En utilisant ensuite les coordonnées du point $C$ et en procédant de la même manière que précédemment, on trouve que l'équation réduite de la droite cherchée est \dresultat {y = -{1\over 3} x + 4}. \fincorrige