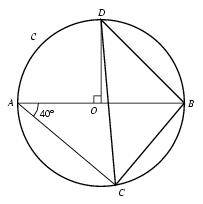
\exo {Cercles, triangles et angles} On note $\cal C$ le cercle de centre $O$ et de diamètre $[AB]$. Les points $C$ et $D$ sont disposés comme l'indique la figure ci-dessous~: $$ \widehat {BOD} = 90°, \qquad {\rm et} \qquad \widehat {BAC} = 40°. $$ \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/config/} $$ \superboxepsillustrate {cerc_001.ps} $$ Calculer les mesures des angles du triangle $BCD$. \finexo \corrige Les angles $\widehat {CAB}$ et $\widehat {CDB}$ sont deux angles inscrits interceptant le même arc, donc ils sont de même mesure et \dresultat {\widehat {CDB} = 40°}. Le triangle $ODB$ est un triangle rectangle par hypothèse, et il est isocèle puisque $OD$ et $OB$ sont des rayons du cercle~$\cal C$. On a donc en particulier \dresultat {\widehat {OBD} = 45°}. Le triangle $ABC$ est rectangle en $C$ puisque $A$, $B$ et $C$ sont des point du cercle $\cal C$ alors que $[AB]$est un diamètre de $\cal C$. La somme des angles étant de $180°$ dans un triangle, on en déduit que \dresultat {\widehat {ABC} = 50°}. En raisonnant maintenant dans le triangle $BDC$, on trouve l'angle manquant~: \dresultat {\widehat {DCB} = 180 - 135 = 45°}. \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/config/} $$ \superboxepsillustrate {cerc_001b.ps} $$ On peut alors conclure $$ \dresultat {\widehat {CDB} = 40°} \qquad \qquad \dresultat {\widehat {DBC} = 95°} \qquad {\rm et}\qquad \dresultat {\widehat {BCD} = 45°} $$ \fincorrige