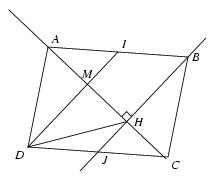
\exo {Parallélogramme et triangle isocèle} \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/config/} Dans le parallélogramme $ABCD$ ci-dessous~: \itemitem {--} $I$ et $J$ sont les milieux respectifs des segments $[AB]$ et $[CD]$~; \itemitem {--} $H$ est le pied de la perpendiculaire à la droite $(BJ)$ passant par $A$~; \itemitem {--} $M$ est l'intersection des droites $(DI)$ et $(AH)$. {\sl Le but de l'exercice est de démontrer que le triangle $AHD$ est isocèle}. $$ \superboxepsillustrate {parall_001.ps} $$ \itemnum Démontrer que le quadrilatère $DJBI$ est un parallélogramme. \itemnum Démontrer que les droites $(AH)$ et $(DI)$ sont perpendiculaires. \itemnum Montrer que la droite $(DI)$ est la médiatrice du segment $[AH]$. \itemnum Conclure. \finexo \corrige \itemnum On a \dresultat {(IB) \parallel (DJ)} puisque $ABCD$ parallélogramme avec $I\in (AB)$ et $J\in (DC)$. Et on a \dresultat {IB = DJ} puisque ces 2~longueurs sont égales à ${1\over 2} AB$ (car $I$ et $J$ milieux respectifs de $[AB]$ et $[DC]$ par hypothèse). \item {} Le quadrilatère \tresultat {$DJBI$ est donc un parallélogramme} puisqu'il a deux côtés opposés parallèles et de même longueur. \itemnum Le fait que $DJBI$ soit un parallèlogramme implique en particulier que \dresultat {(DI) \parallel (BJ)}, ce qui prouve que \dresultat {(AH) \perp (DI)} puisque $(AH)$ perpendiculaire à $(BJ)$ par hypothèse (lorsque 2 droites sont parallèles, toute perpendiculaire à l'une est perpendiculaire à l'autre). \itemnum Dans le triangle $ABH$, le point \tresultat {$I$ est le milieu de $[AB]$} (par hypothèse) et \tresultat {$(BH)$ est parallèle à $(IM)$} (puisque $(ID) \parallel (BJ)$ d'après la question {\bf 1.} et que l'on a $H\in (BJ)$ et $M \in (ID)$). Le théorème des milieux permet de conclure que \tresultat {$M$ est le milieu de $[AH]$}. \item {} Finalement, la droite $(DI)$ est perpendiculaire à $(AH)$ (d'après la question {\bf 2.}) et elle passe par le milieu de $[AH]$. C'est donc \tresultat {la médiatrice de $[AH]$}. \itemnum Pour finir, et par définition de la médiatrice, tout point de la médiatrice de $[AH]$ est à égale distance des points $A$ et $H$. Le point $D$ étant sur cette médiatrice, on a $AD = DH$ et \tresultat {le triangle $ADH$ est isocèle}. \fincorrige