thales_001.tex

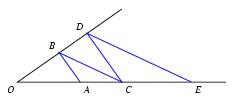
\exo {Calcul de longueur}
 
Dans la figure ci-dessous, on donne
$OA = 3\cm $, $AC = 2\cm $, $(AB)$ et $(CD)$ parallèles, $(BC)$ et
$(DE)$ parallèles.
\def \epspath {%
   $HOME/tex_doc/lycee/database/2nd/geometrie/config/}
$$
   \superboxepsillustrate {thales_001.ps}
$$
 
Calculer la longueur $CE$.
 
\finexo
 
\corrige
 
\def \epspath {%
   $HOME/tex_doc/lycee/database/2nd/geometrie/config/}
$$
   \superboxepsillustrate {thales_001b.ps}
$$
Les droites $(AB)$  et $(CD)$ étant parallèles, les triangles $OAB$ et
$OCD$ sont en configuration de Thalès. On en déduit en particulier
$$
   {OB\over OD} = {OA\over AC} = {3\over 5}.
$$
De la même façon, les droites $(CB)$  et $(ED)$ étant parallèles, les
triangles $OCB$ et $OED$ sont en configuration de Thalès. On en déduit
en particulier
$$
   {OC\over OE} = {OB\over OD} = {3\over 5}
      \qquad {\rm d'où} \qquad
   OE = {5\over 3} \times OC
      \qquad {\rm d'où} \qquad
   OE = {25\over 3}.
$$
Finalement, 
$$
   CE = OE - OC = {25\over 3} - 5
      \qquad {\rm soit} \qquad
   \dresultat {CE = {10\over 3}}.
$$
\fincorrige