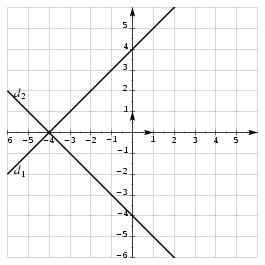
\exo {Droites~: un exercice de synthèse} \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/droites/} \itemitemalphnum Lire sur le graphique ci-dessous une équation de chacune des droites $d_1$ et $d_2$. \itemitemalph Montrer que les droites $d_1$ et $d_2$ sont perpendiculaires. $$ \epsillustrate {synt_001.ps} $$ \itemnum On considère les droites $d_3$ et $d_4$ d'équations respectives $$ d_3~: \quad y = 5 -2x \qquad \qquad d_4~: \quad 2y -2x + 2 = 0 $$ \itemitemalph Vérifier que le point $A (-1; -2)$ appartient à la droite $d_4$. \itemitemalph Montrer que $d_1$ et $d_4$ sont parallèles. \itemitemalph Représenter les droites $d_3$ et $d_4$ sur le graphique ci-dessus. \itemnum Déterminer les coordonnées de $B$, le point d'intersection des droites $d_3$ et $d_4$. \itemnum Déterminer une équation de $d_5$, la perpendiculaire à $d_4$ passant par $B$. \finexo \corrige {} \itemalphnum Sur le graphique on lit facilement les deux ordonnées à l'origine~: $4$ pour $d_1$ et $-4$ pour $d_2$. Quand aux coefficients directeurs, il est facile de voir que les vecteurs $$ \pmatrix {1\cr 1\cr } \qquad {\rm et} \qquad \pmatrix {1\cr -1\cr } $$ sont respectivement des vecteurs directeurs des droites $d_1$ et $d_2$. D'où les coefficients directeurs cherchés~: $1$ pour $d_1$ et $-1$ pour $d_2$. Finalement, les 2~équations cherchées sont~: $$ \dresultat {d_1~: y = x+4} \qquad {\rm et} \qquad \dresultat {d_2~: y = -x-4} $$ \itemalph On en déduit sans peine que \tresultat {les droites $d_1$ et $d_2$ sont perpendiculaires} puisque le produit de leurs coefficients directeurs est égal à $-1$. \itemalphnum Une équation de $d_4$ est $2y-2x+2=0$, et on a bien $2\times (-2) - 2\times (-1) + 2 = 0$. Donc les coordonnées du point $A$ vérifient l'équation de la droite $d_4$, ce qui prouve que \tresultat {$A$ appartient à $d_4$}. \itemalph L'équation réduite de $d_1$ obtenue dans le {\bf 1.} nous donne immédiatement son coefficient directeur~: $-2$. Pour la droite $d_4$, on a $$ 2y - 2x + 2 = 0 \quad \Longleftrightarrow \quad 2y = 2x - 2 \quad \Longleftrightarrow \quad \dresultat {d_4~: y = x - 1} $$ d'où le coefficient directeur de $d_4$~: $1$. Ces deux droites ont le même coefficient directeur, ce qui prouve que \dresultat {d_1 /\!/ d_4} \itemalph \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/droites/} $$ \epsillustrate {synt_001b.ps} $$ \itemnum Chercher l'intersection des droites $d_3$ et $d_4$ revient à résoudre le système $$ \cases { y = 5-2x \cr 2y-2x+2=0 \cr } \quad \Longleftrightarrow \quad \matrix { \scriptstyle (1) \cr \scriptstyle (2) \cr } \cases { y + 2x = 5 \cr 2y - 2x = -2 \cr } \quad \Longleftrightarrow \quad \matrix { \scriptstyle (1) \cr \scriptstyle (1) + (2) \cr } \cases { y + 2x = 5 \cr 3y = 3 \cr } \quad \Longleftrightarrow \quad \cases { x = 2 \cr y = 1 \cr } $$ d'où \tresultat {l'unique point d'intersection~: $B (2, 1)$}. \itemnum Le coefficient directeur de $d_4$ étant $1$ d'après le {\bf 2.}{\sl b\/}), celui d'une perpendiculaire à $d_4$ sera de $-1$ (produit des coeffs égal à $-1$). Donc $d_5$ admet une équation du type $y = -x + p$. Or le point $B$ appartient à $d_5$, et donc ses coordonnées vérifient l'équation de $d_5$. D'où la relation $1 = -2+p$ d'où l'on tire $p = 3$. Finalement, l'équation cherchée est \dresultat {d_5~: y = -x+3}. \fincorrige