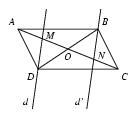
\exo {Démontrer avec une symétrie centrale} On considère $ABCD$, un parallélogramme de centre $O$. On note $d$ une droite passant par $D$ qui coupe le segment $[AC]$ en $M$ et on appelle $d'$ la parallèle à $d$ passant par $B$ qui coupe le segment $[AC]$ en $N$. \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/transform/} $$ \epsillustrate {demo_001.ps} $$ \itemnum Démontrer que $d'$ est l'image de $d$ par la symétrie $s$ de centre $O$. \itemnum Démonter que $O$ est le milieu de $[MN]$. \finexo \corrige \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/transform/} $$ \epsillustrate {demo_001a.ps} $$ \itemnum On remarque tout d'abord que $s (D) = B$ puisque $O$ milieu de $[BD]$. \item {} On sait que pour une symétrie centrale, l'image d'une droite est une droite parallèle à la droite d'origine. Or la droite $d$ passe par le point $D$ (par hypothèse), donc l'image de $d$ passe par le point image de $D$, c'est à dire $B$. \item {} Conclusion~: $s (d)$ est une droite parallèle à $d$ qui passe par $B$. Autrement dit \dresultat {s (d) = d'}. \itemnum Il est clair que l'on a $s (A) = C$ et $s (C) = A$ (puisque $O$ milieu de $[AC]$). Donc par $s$, l'image de la droite $(AC)$ est elle-même, autrement dit $s (d'') = (d'')$ si l'on note $d''$ la droite $(AC)$. \item {} Le point $M$ est l'intersection de $d$ et de $d''$, donc le point $s (M)$ sera l'intersection de $s (d)$ et de $s (d'')$ (conservation du point d'intersection), autrement dit de $d'$ et $d''$ (en vertu des questions précédentes). D'où \dresultat {s (M) = N}, ce qui prouve que \tresultat {$O$ est le milieu de $[MN]$}. \fincorrige