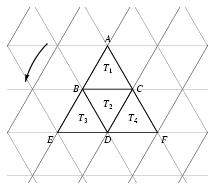
\exo {Reconnaître une transformation} La figure ci-dessous est dessinée dans un réseau régulier formé des triangles équilatéraux dont certains sont notés $T_1$, $T_2$, $T_3$, $T_4$. \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/transform/} $$ \superboxepsillustrate {tp_001.ps} $$ Pour chacune des questions suivantes, la réponse sera donnée sans justification. \itemitemalphnum Quel est l'axe de la symétrie orthogonale qui transforme $T_1$ en $T_2$~? \itemitemalph Quel est le vecteur de la translation qui tranforme $T_1$ en $T_3$~? \itemitemalph Quel est le centre de la symétrie centrale qui transforme $T_2$ en $T_4$~? \itemnum $T_1$ a pour image $T_2$ par une rotation de centre $C$ qui transforme $A$ en $B$ dans le sens de la flèche. Quel est l'angle de cette rotation~? \itemnum On note $S$ la symétrie orthogonale d'axe $(CD)$, $t$ la translation de vecteur $\overrightarrow {CA}$ et $s$ la symétrie centrale dont le centre est le milieu de $[CD]$. \item {} On transforme $T_3$ par $S$, puis l'image obtenue par $t$, puis enfin la nouvelle image obtenue par $s$. \item {} \` A quel triangle aboutit-on~? \finexo