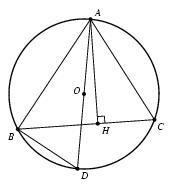
\exo {Cercle et triangles semblables} Soit $\cal C$ un cercle de centre $O$ et de rayon $r$. On considère $ABC$, un triangle inscrit dans le cercle $\cal C$ et tel que l'angle $\widehat {BAC}$ soit aigu. On nomme $H$ le projeté orthogonal de $A$ sur $[BC]$, et $D$ le point où la droite $(AO)$ recoupe $\cal C$. On note $D$ un point de l'arc $\widehat {BC}$ ne contenant pas $A$, et $E$ le point d'intersection de la droite $(AD)$ et du segment $[BC]$. \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/triangle/} $$ \superboxepsillustrate {sembl_003.ps} $$ \itemnum Démontrer que les triangles $DBE$ et $CAE$ sont semblables. \itemnum On pose $AB = c$, $AC = b$, et $AH = h$. \item {} Déduire de la question précédente que $bc = 2rh$. \finexo \corrige \itemnum Les points $A$, $B$, $C$, $D$ sont sur le même cercles, et les angles $\widehat {BDA}$ et $\widehat {BCA}$ interceptent le même arc de cercle $AB$. Donc $\widehat {BDA} = \widehat {BCA}$, soit \dresultat {\widehat {D} = \widehat {C}}. De plus, les angles $\widehat {BED}$ et $\widehat {AEC}$ sont opposés par les sommet, dont \dresultat {\widehat {BED} = \widehat {AEC}}. \item {} Finalement, les triangles $DBE$ et $CAE$ ont deux angles deux à deux égaux, ce qui prouve qu'\tresultat {ils sont semblables}. \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/triangle/} $$ \superboxepsillustrate {sembl_003a.ps} $$ \itemnum On remarque que $[AD]$ est un diamètre du cercle $\cal C$ et $B$ est un point de ce cercle, donc $ABD$ est un triangle rectangle en $B$, d'où \dresultat {\widehat {ABD} = 90° = \widehat {AHC}}. Les deux triangles \tresultat {$ABD$ et $AHC$} sont donc semblables puisqu'ils ont deux angles égaux deux à deux \item {} Maintenant, dans les triangles semblables $ABD$ et $AHC$, on a $$ {AB\over AH} = {c\over h} = {AD\over AC} = {2r\over b} \qquad \hbox {et donc} \qquad \dresultat {bc = 2rh}. $$ \fincorrige