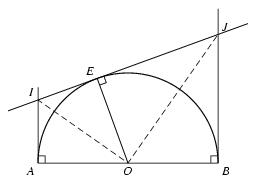
\exo {Tangentes à un cercle, triangles semblables} \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/triangle/} Sur la figure ci-dessous, $E$ est un point du demi-cercle $\cal C$ de diamètre $[AB]$ er de rayon $R$. La tangente en $E$ à $\cal C$ coupe la tangente en $A$ à $\cal C$ en $I$ et la tangente en $B$ à $\cal C$ en $J$. $$ \superboxepsillustrate {sembl_010.ps} $$ \itemitemalphnum Montrer que les triangles $OAI$ et $OEI$ sont isométriques. \itemitem {} Citer sans justifier deux autres triangles isométriques. \itemitemalph En déduire que le triangle $IOJ$ est rectangle. \itemitemalphnum Montrer que les triangles $OEI$ et $OEJ$ sont semblables. \itemitemalph En déduire que $$ IE \times EJ = R^2, \qquad \hbox {puis que} \qquad AI \times BJ = R^2. $$ \finexo \corrige \itemalphnum Les triangles $OAI$ et $OEI$ ont le \tresultat {côté $OI$ en commun}. De plus \dresultat {OA = OE} puisque ce sont 2~rayons du demi-cercle. Pour finir, on remarque que $OAI$ et $OEI$ sont par hypothèse des triangles rectangles, et le théorème de Pythagore permet facilement de conclure à l'égalité \dresultat {AI = IE} puisque l'on a l'égalité des hypothénuses et de l'un des côtés. Plus précisément, $$ AI = \sqrt {OI^2 - OA^2} = \sqrt {OI^2 - OE^2} = IE $$ \item {} Finalement, les triangles \tresultat {$OAI$ et $OEI$ sont isométriques} puisqu'ils ont trois côtés égaux 2~à~2. \item {} Une démonstration tout à fait analogue prouverait que les triangles \tresultat {$OEI$ et $OBI$ sont isométriques}. \epsfxsize 60mm \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/triangle/} $$ \superboxepsillustrate {sembl_010a.ps} $$ \itemalph Les triangles $OAI$ et $OEI$ étant isométriques, ils sont en particulier semblables et ils ont les mêmes angles. En particulier, on a \dresultat {\widehat {AOI} = \widehat {IOE}}. On notera $x = \widehat {AOI}$. \item {} Un raisonnement analogue pour les triangles $OEI$ et $OBI$ prouve que \dresultat {\widehat {EOI} = \widehat {IOB}}. On notera $y = \widehat {EOI}$. \item {} Il est alors clair que $2 x + 2y = 180$, et donc $x+y = 90$ or $\widehat {IOJ} = x +y$. On a donc finalement prouvé que \dresultat {\widehat {IOJ} = 90}, autrement dit que le triangle \tresultat {$IOJ$ est rectangle}. \itemalphnum Dans un triangle, la somme des angles fait $180°$. Appliqué au triangle $OEI$, et en se rappelant que $x+y = 90$, on voit que \dresultat {\widehat {EIO} = x}. De la même manière, dans le triangle $OAI$, on a clairement \dresultat {\widehat {OIA} = y}. \item {} Finalement, les triangles $OEI$ et $OEJ$ ont trois angles égaux 2~à~2 (de mesures respectives, $x$, $y$ et $90$), ce qui prouve qu'\tresultat {ils sont semblables}. \itemalph Les triangles $OEI$ et $OEJ$ étant semblables, on a les égalités de rapports $$ {EJ\over OE} = {OJ\over OI} = {OE\over IE} \qquad {\rm or} \qquad OE = OA = R $$ et donc en particulier $$ {EJ\over R} = {R\over IE} \qquad {\rm or} \qquad \dresultat {EJ \times IE = R^2} $$ On se rappelle ensuite que les triangles $OAI$ et $OEI$ étant isométriques (d'après question {\bf 1.}), on a $EI = AI$, puis, de la même façon, que $EJ = BJ$ puisque $OEI$ et $OBI$ sont isométriques (toujours d'après question {\bf 1.}). En reportant dans l'égalité précédente, on a alors \dresultat {AI\times BJ = R^2}. \fincorrige