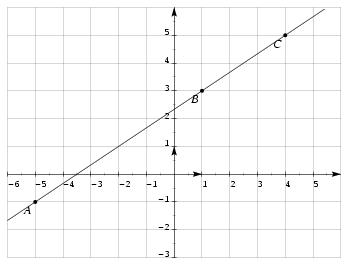
\exo {Coordonnées et alignement de points} Dans le plan muni d'un repère $(O, \vec \imath , \vec \jmath )$, on considère les points $$ A (-5; -1) \qquad \qquad B (1; 3) \qquad \qquad C (4; 5). $$ \itemnum Placer les points $A$ $B$ et $C$ dans le repère ci-dessous \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/vecteurs/} $$ \superboxepsillustrate {align_003a.ps} $$ \itemnum Les points $A$, $B$ et $C$ sont-ils alignés~? (Justifier la réponse par un calcul.) \finexo \corrige {} \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/vecteurs/} \itemnum $$ \superboxepsillustrate {align_003.ps} $$ \itemnum Les points $A$, $B$ et $C$ sont alignés si et seulement si les vecteurs $\overrightarrow {AB}$ et $\overrightarrow {AC}$ sont colinéaires. Calculons les coordonnées de ces deux vecteurs~: $$ \overrightarrow {AB} = \pmatrix {1+5\cr 3+1\cr } = \pmatrix {6\cr 4\cr } \qquad {\rm et} \qquad \overrightarrow {AC} = \pmatrix {4+5\cr 5+1\cr } = \pmatrix {9\cr 6\cr } $$ On s'aperçoit alors que \dresultat {\overrightarrow {AC} = {3\over 2}\overrightarrow {AB}}, ce qui prouve que les points \tresultat {$A$, $B$ et $C$ sont alignés}. Une autre méthode (que vous ne connaissiez pas au moment de ce devoir, mais que vous allez apprendre pour lundi prochain), consiste à utiliser la propriété suivante~: \assert Propriété . $$ \vec u \pmatrix {x\cr y\cr } \quad {\rm et} \quad \vec v \pmatrix {x'\cr y'\cr } \quad \hbox {sont colinéaires} \qquad \iff \qquad xy - x'y' = 0. $$ \endassert \item {} Ici, après avoir calculé les coordonnées des vecteurs $\overrightarrow {AB}$ et $\overrightarrow {AC}$, l'utilisation de cette propriété donne $6\times 6 - 9\times 4 = 0$, ce qui prouve que \tresultat {les vecteurs $\overrightarrow {AB}$ et $\overrightarrow {AC}$ sont colinéaires}, ce qui permet de conclure. \fincorrige