calc_012.tex

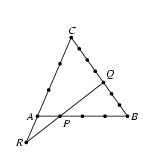
\exo {Calcul vectoriel}
 
On considère le triangle $ABC$. $P$ est un point de $(AB)$, $Q$ un
point de $BC$ et $R$ un point de $AC$, disposés comme sur le dessin.
(Les graduations sur les droites sont régulières.)
 
\itemnum Donner les valeurs des réels $\alpha $, $\beta $ et $\gamma $
tels que~:
$$
   \overrightarrow {AP} = \alpha \overrightarrow {AB},
      \qquad \qquad
   \overrightarrow {AR} = \beta \overrightarrow {AC},
      \qquad {\rm et} \qquad
   \overrightarrow {BQ} = \gamma \overrightarrow {BC}.
$$
 
\itemnum Exprimer $\overrightarrow {PR}$ en fonction de
      $\overrightarrow {AB}$ et $\overrightarrow {AC}$.
 
\itemnum Démontrer que
$$
   \overrightarrow {PQ} = {9\over 28}\overrightarrow {AB} + {3\over 7}\overrightarrow {AC}.
$$
 
\itemnum Justifier que
$$
   \overrightarrow {PQ} = -{9\over 7}\overrightarrow {PR}.
$$
Que peut-on en conclure~?
 
\def \epspath {%
   $HOME/tex_doc/lycee/database/2nd/geometrie/vecteurs/}
$$
   \superboxepsillustrate {calc_012.ps}
$$
 
\finexo
 
\corrige
 
\itemnum On lit sur le dessin 
\dresultat {\alpha = {1\over 4}},
\dresultat {\beta = -{1\over 3}},
et \dresultat {\gamma = {3\over 7}}. Autrement dit, on a
$$
   \overrightarrow {AP} = {1\over 4} \overrightarrow {AB},
      \qquad \qquad
   \overrightarrow {AR} = -{1\over 3}\overrightarrow {AC},
      \qquad {\rm et} \qquad
   \overrightarrow {BQ} = {3\over 7}\overrightarrow {BC}.
$$
 
\itemnum En utilisant la relation de Chasles, il vient
$$
   \overrightarrow {PR} 
      = \overrightarrow {PA} + \overrightarrow {AR}
      \qquad {\rm soit} \qquad
   \dresultat {\overrightarrow {PR} 
      = -{1\over 4}\overrightarrow {AB} -{1\over 3} \overrightarrow {AC}}
$$
 
\itemnum Utilisons encore la relation de Chasles. On a
$$\eqalign {
   \overrightarrow {PQ} 
      &= \overrightarrow {PA} + \overrightarrow {AB} + \overrightarrow {BQ}
\cr
      &= -{1\over 4}\overrightarrow {AB} + \overrightarrow {AB} 
      + {3\over 7}\overrightarrow {BC}
\cr
      &= \left( -{1\over 4}+1\right) \overrightarrow {AB} +
      {3\over 7} (\overrightarrow {BA} + \overrightarrow {AC})
\cr
      &= {3\over 4} \overrightarrow {AB} - {3\over 7} \overrightarrow {AB} 
      + {3\over 7} \overrightarrow {AC}
\cr
      &= \left( {3\over 4} - {3\over 7}\right) \overrightarrow {AB} +
      + {3\over 7} \overrightarrow {AC}.
      \qquad {\rm soit} \qquad
   \dresultat {\overrightarrow {PQ} = {9\over 28}\overrightarrow {AB} +
      {3\over 7}\overrightarrow {AC}}.
\cr
}$$
 
\itemnum Utilisons maintenant la relation du {\bf 2.} et multiplions
la par $-9/7$. Il vient
$$
   -{9\over 7}\overrightarrow {PR} 
      = -{9\over 7} \times {-1\over 4}\overrightarrow {AB} 
      -{9\over 7} \times {-1\over 3} \overrightarrow {AC}
      \quad {\rm soit} \quad
   -{9\over 7}\overrightarrow {PR} = {9\over 28}\overrightarrow {AB} +
      {3\over 7}\overrightarrow {AC}
      \quad {\rm d'où} \quad   
   \dresultat {\overrightarrow {PQ} = -{9\over 7}\overrightarrow {PR}}.
$$
On en conclut que les vecteurs \tresultat {$\overrightarrow {PQ}$ et
$\overrightarrow {PR}$ sont colinéaires}, et, par suite, que les points
\tresultat {$P$, $Q$ et $R$ sont alignés}.
 
\fincorrige