config_001.tex

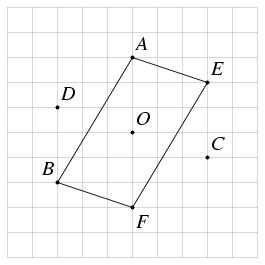
\exo {Démontrer avec des vecteurs (milieu et parallélogramme)}
 
On considère un triangle $BOA$, et on note $D$ et $C$ les points tels
que
$$
   \overrightarrow {OD} = \overrightarrow {OA} + \overrightarrow {OB} 
      \qquad {\rm et} \qquad
   \overrightarrow {OA} + \overrightarrow {OB}  + \overrightarrow {OC} =
      \vec 0.
$$
 
\itemnum Faire un dessin.
 
\itemnum Montrer que $O$ est le milieu de $[CD]$.
 
\itemnum Les points $E$ et $F$ sont tels que
$$
   \overrightarrow {OE} = \overrightarrow {OA} + \overrightarrow {OC} 
      \qquad {\rm et} \qquad
   \overrightarrow {OF} = \overrightarrow {OB} + \overrightarrow {OC}.
$$
 
\itemitemalph Placer les points $E$ et $F$ sur le dessin.
 
\itemitemalph Montrer que $ABFE$ est un parallélogramme.
 
\finexo
 
\corrige {}
 
\def \epspath {%
   $HOME/tex_doc/lycee/database/2nd/geometrie/vecteurs/}
 
\itemnum
\epsfxsize 60mm
$$
   \superboxepsillustrate {config_001.ps}
$$
 
\itemnum On a par hypothèse
$$
   \overrightarrow {OD} = \overrightarrow {OA} + \overrightarrow {OB} 
      \qquad {\rm et} \qquad
   \overrightarrow {OA} + \overrightarrow {OB}  + \overrightarrow {OC} =
      \vec 0.
$$
On en déduit alors que \dresultat {\overrightarrow {OD} +
\overrightarrow {OC} = \vec 0}, ce qui prouve que \tresultat {$O$ est
le milieu de $[CD]$}.
 
\itemnum On sait par hypothèse que $\overrightarrow {OE} =
\overrightarrow {OA} + \overrightarrow {OC}$. On en déduit que
$$
   \overrightarrow {OC} = \overrightarrow {OE} - \overrightarrow {OA} 
      = \overrightarrow {OE} + \overrightarrow {AO} 
      = \overrightarrow {AO} + \overrightarrow {OE} 
      = \overrightarrow {AE}
      \qquad {\rm soit} \qquad
   \overrightarrow {OC}= \overrightarrow {AE}
$$
Et de la même façon, sachant par hypothèse que
$\overrightarrow {OF} = \overrightarrow {OB} + \overrightarrow {OC}$,
on en déduit
$$
   \overrightarrow {OC} = \overrightarrow {OF} - \overrightarrow {OB} 
      = \overrightarrow {OF} + \overrightarrow {BO} 
      = \overrightarrow {BO} + \overrightarrow {OF} 
      = \overrightarrow {BF}
      \qquad {\rm soit} \qquad
   \overrightarrow {OC}= \overrightarrow {BF}
$$
Finalement, on a donc \dresultat {\overrightarrow {AE}=
\overrightarrow {BF}}, ce qui prouve que \tresultat {$ABFE$ est un
parallélogramme}.
 
\fincorrige