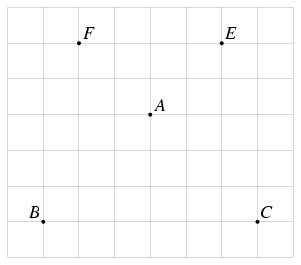
\exo {Démontrer avec des vecteurs} On considère un triangle $ABC$. \itemnum Construire les points $E$ et $F$ définis par $$ \overrightarrow {AE} = - {2\over 3}\overrightarrow {AB} \qquad {\rm et} \qquad \overrightarrow {AF} = - {2\over 3}\overrightarrow {AC}. $$ \itemnum Exprimer $\overrightarrow {EF}$ en fonction de $\overrightarrow {BC}$. \itemnum En déduire que les droites $(EF)$ et $BC$ sont parallèles. \finexo \corrige {} \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/vecteurs/} \itemnum \epsfxsize 60mm $$ \superboxepsillustrate {paral_001.ps} $$ \itemnum On a $$\eqalign { \overrightarrow {EF} &= \overrightarrow {EA} + \overrightarrow {AF} = {2\over 3} \overrightarrow {AB} - {2\over 3} \overrightarrow {AC} \cr &= {2\over 3} \overrightarrow {AB} + {2\over 3} \overrightarrow {CA} \cr &= {2\over 3} \left( \overrightarrow {CA} + \overrightarrow {AB} \right) \qquad {\rm soit} \qquad \dresultat {\overrightarrow {EF} = {2\over 3} \overrightarrow {CB} = -{2\over 3} \overrightarrow {BC}} \cr }$$ \itemnum Les vecteurs $\overrightarrow {EF}$ et $-{2\over 3} \overrightarrow {BC}$ sont égaux. Ils ont donc en particulier la même direction, ce qui signifie qu'ils sont porté par des droites parallèles. On en déduit que \dresultat {(EF) \parallel (BC)}. \fincorrige