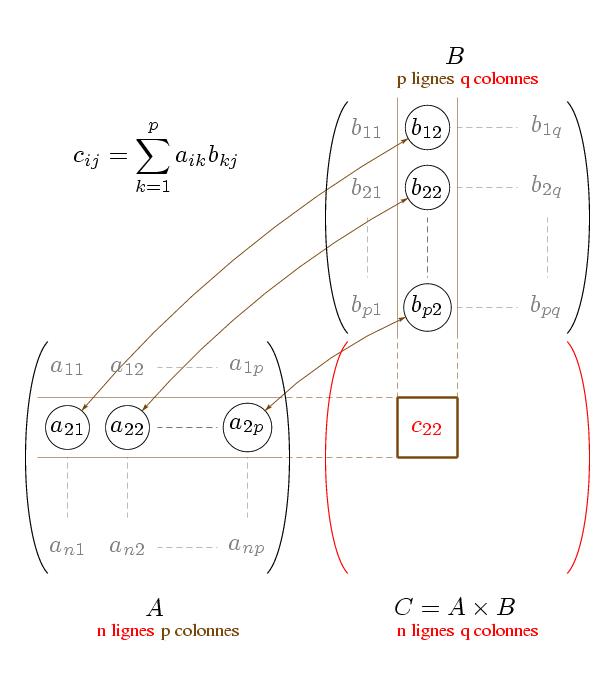
\paragraphe{Calcul matriciel élémentaire} \sparagraphe{Addition de 2~matrices} Soit $A = (a_{ij})$ et $B = (b_{ij})$ deux matrices $(n, p)$ (c'est à dire $n$ lignes et $p$ colonnes). La matrice $A + B = (c_{ij})$ est la matrice $(n, p)$ telle que, pour tout couple d'indices $(i, j)$ vérifiant $1 \leq i \leq n$ et $1 \leq j \leq p$, on ait $$ c_{ij} = a_{ij} + b_{ij}. $$ Par exemple, $$ \pmatrix{ 1 & 2 & 3 \cr 4 & 5 & 6 \cr} + \pmatrix{ 7 & 8 & 9 \cr 10 & 11 & 12 \cr} = \pmatrix{ 8 & 10 & 12 \cr 14 & 16 & 18} $$ \sparagraphe{Produit d'une matrice par un réel} Soit $A = (a_{ij})$ une matrices $(n, p)$ et $\lambda$ un réel quelconque. La matrice $\lambda \cdot A = (c_{ij})$ est la matrice $(n, p)$ telle que, pour tout couple d'indices $(i, j)$ vérifiant $1 \leq i \leq n$ et $1 \leq j \leq p$, on ait $$ c_{ij} = \lambda a_{ij}. $$ Par exemple, $$ 2 \cdot \pmatrix{ 1 & 2 & 3 \cr 4 & 5 & 6 \cr} = \pmatrix{ 2 & 4 & 6\cr 8 & 10 & 12} $$ \sparagraphe{Produit de 2~matrices} Soit $A = (a_{ij})$ une matrices $(n, p)$ et $B = (b_{ij})$ une matrices $(p, q)$. La matrice $A \times B = (c_{ij})$ est la matrice $(n, q)$ telle que, pour tout couple d'indices $(i, j)$ vérifiant $1 \leq i \leq n$ et $1 \leq j \leq q$, on ait $$ c_{ij} = \sum_{k = 1}^p \big( a_{ik} \cdot b_{kj} \big) = a_{i1} b_{1j} + a_{i2} b_{2j} + \cdots + a_{ip} b_{pj} . $$ \def \epspath {% $HOME/tex_doc/lycee/database/btsmai/algebre/linear/} \epsfxsize 50mm $$ \epsillustrate {cours_06.ps} $$ Ainsi, par exemple, on a $$ \pmatrix{ 1 & 2 \cr 3 & 4 \cr 5 & 6 \cr} \times \pmatrix{ 7 & 8 \cr 9 & 10 \cr} = \pmatrix{ 1 \times 7 + 2 \times 9 & 1 \times 8 + 2 \times 10 \cr 3 \times 7 + 4 \times 9 & 3 \times 8 + 4 \times 10 \cr 5 \times 7 + 6 \times 9 & 5 \times 8 + 6 \times 10 \cr} = \pmatrix{ 25 & 28 \cr 57 & 64 \cr 89 & 100 \cr} $$ \remarque Pour le calcul du coefficient $a_{ij}$, on utilise donc la $i^{\rm ème}$~ligne de la première matrice, et la $j^{\rm ème}$~colonne de la deuxième matrice. \finremarque \sparagraphe{Propriétés} On retrouve des propriétés analogues à certaines bien connues dans $\rset$~: si $\lambda$ est un réel quelconque et $A$, $B$ et $C$ trois matrices telles que les opérations ci-dessous aient un sens, on a \itemitem{$\bullet$} $A \times (B \times C) = (A \times B) \times C$ \itemitem{$\bullet$} $A \times (B + C) = (A \times B) + (A\times C)$ \itemitem{$\bullet$} $A \times (\lambda B) = (\lambda A) \times B = \lambda \cdot (A \times B)$ ATTENTION, la multiplication des matrices n'est pas commutative~: on a $$ A \times B \neq B \times A \qquad \hbox{en général} $$