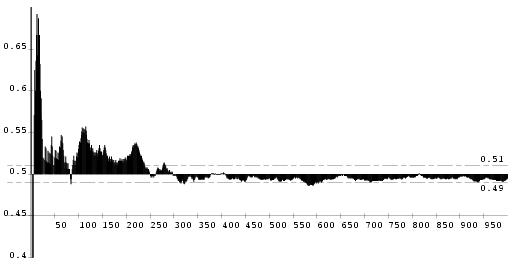
\paragraphe{Introduction~: lien fréquence $\leftrightarrow$ probabilité} Il a fallu longtemps pour arriver à une définition satisfaisante de la probabilité. Celle en vigueur actuellement a été publiée en $\oldstyle 1933$ et est due au russe Kolmogorov. Cette définition explicite le lien entre la fréquence d'un événement et sa probabilité. Elle s'exprime de façon tout à fait rigoureuse (bien sûr), et en français vulgarisé elle dit à peu près ceci~: {\sl Plus le nombre d'expérience augmente, et plus il est {\bf probable} que la fréquence de l'événement $A$ sera proche de la probabilité de $A$.} \def \epspath {% $HOME/tex_doc/lycee/database//btsmai/algebre/proba/} \epsfxsize = 150mm Par exemple, au jeu de {\sl Pile ou Face}, la probabilité de l'événement \og {\sl obtenir un Pile}\fg \ est $1/2$. Cela signifie que plus le nombre de parties augmente, et plus il est probable que la fréquence d'apparition du {\sl Pile\/} soit proche de $1/2$. Dans la pratique, on obtient des schémas où l'on observe une certaine \og stabilisation de la fréquence\fg \ avec l'augmentation du nombre d'expériences. Par exemple, en voici un issu d'une simulation de $1\, 000$~parties successives. $$\displaylines { \superboxepsillustrate {cour_008.ps} \cr \matrix { \hbox {Simulation du jeu de Pile ou Face sur $1\, 000$ parties} \cr \hbox {évolution de la fréquence d'apparition du Pile} } \cr } $$ Sur $100\, 000$~parties, on obtient un graphique de ce type (noter le facteur d'agrandissement par rapport au graphique précédent)~: % \epsfxsize = 160mm % $$\displaylines { \superboxepsillustrate {cour_008b.ps} \cr \matrix { \hbox {Simulation du jeu de Pile ou Face sur $100\, 000$ parties} \cr \hbox {évolution de la fréquence d'apparition du Pile} } \cr } $$ Cette définition est évidemment inexploitable telle quelle à notre niveau, bien qu'il soit possible (et donc {\sl probable}), que nous la retrouvions plus tard dans l'année scolaire. Sous sa forme rigoureuse, elle est appelée {\sl loi faible des grands nombres}.