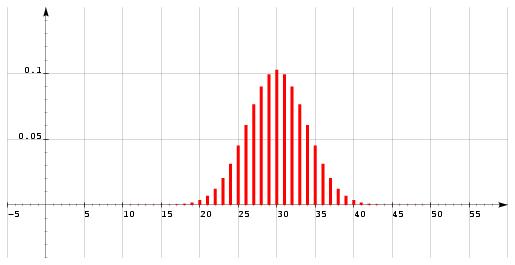
\def \epspath{% $HOME/tex_doc/lycee/database/btsmai/algebre/proba/} \paragraphe{Loi binômiale (épreuves indépendantes répétées)} On considère une expérience aléatoire n'ayant que {\bf deux issues possibles}~: $A$ et $\overline A$ (souvent appelés {\sl succès\/} et {\sl échec\/}), et on répète $n$ fois de suite cette expérience, en faisant l'hypothèse que chaque expérience est {\bf indépendante des précédentes} (cas du jeu de Pile ou Face par exemple). On dit que l'on est dans le cadre d'un {\sl schéma de Bernouilli}. On note $p$ la probabilité de $A$ et $q = 1-p$ la probabilité de $\overline A$. On note $X$ la variable aléatoire indiquant le nombre de fois où $A$ est réalisé après les $n$ expériences. Alors la loi de probabilité de $X$, notée ${\cal B} (n, p)$, est appelée {\sl loi binômiale de paramètres $n$ et $p$}, et elle est caractérisée par $$\dresultat{ p (X = k) = C_n^k p^k (1-p)^{n-k} = C_n^k p^k q^{n-k} }$$ On montre alors que son espérance, sa variance et son écart-type vérifient $$ \dresultat{E (X) = np} \qquad \qquad \dresultat{V (X) = npq} \qquad \qquad \dresultat{\sigma (X) = \sqrt{npq}} $$ \assert Exemple~: Jeu de Pile ou Face. On lance une pièce de monnaie 60 fois de suite, et on appelle $X$ la variable aléatoire qui, à chaque série de 60~lancers, associe nombre de fois où est sorti le {\sl Pile}. Chaque lancer est indépendant des précédents, et il n'y a que 2~issues possibles ({\sl Pile\/} ou non); la variable aléatoire $X$ suit donc une loi binômiale. Comme la probabilité d'obtenir {\sl Pile\/} est $1/2$, et qu'il y a 60~expériences, cette loi est la loi ${\cal B} (60; 1/2)$ dont la représentation graphique est donnée ci-dessous~: % \epsfxsize = 120mm $$\displaylines{ \superboxepsillustrate{cour_009.ps} \cr \tresultat {loi binômiale $\cal B$ (60; 1/2)} \cr }$$ La probabilité d'obtenir 25~{\sl Pile\/} sur les 60~lancers est $$ p (X=25) = C_{60}^{25} \times \left( {{1\over 2}} \right) ^{25} \times \left( {{1\over 2}} \right) ^{35} \approx 0, 045. $$ \endassert \assert Exemple~: Jeu de dé. On jette un dé bien équilibré à 6~faces. La probabilité d'obtenir le numéro~$\oldstyle 6$ sur un lancer est de $1/6$. On considère l'épreuve qui consiste à lancer 60~fois de suite le dé, en notant à chaque fois le numéro obtenu. On considère maintenant 2~variables aléatoires distinctes~: On note $X$ la variable aléatoire qui à chaque épreuve de 60~lancers associe le nombre de fois où l'on a obtenu le numéro~$\oldstyle 6$, et on note $Y$ la variable aléatoire qui à chaque épreuve de 60~lancers associe le nombre de fois où l'on a {\bf pas} obtenu le numéro~$\oldstyle 6$. Ces 2~variables sont évidemment liées~: quel que soit la série de 60~lancers, on aura $X + Y = 60$. Que ce soit du point de vue de la variable $X$ ou de celui de la variable $Y$, l'expérience consistant à lancer une fois le dé est indépendante des autres expériences, et ne comporte que 2~issues possibles (on obtient le 6 ou pas, le succès du point de vue de $X$ étant l'échec du point de vue de $Y$ et réciproquement). On en déduit que la variable $X$ suit la loi binômiale ${\cal B} (60; 1/6)$ alors que la variable $Y$ suit la loi binômiale ${\cal B} (60; 5/6)$. \newbox \boxone \newbox \boxtwo \setbox \boxone \vbox {% \hsize 70mm \epsfxsize = 60mm $$\displaylines{ \superboxepsillustrate{cour_009a.ps} \cr \tresultat {loi binômiale $\cal B$ (60; 1/6)} \cr }$$ } \setbox \boxtwo \vbox {% \hsize 70mm \epsfxsize = 60mm $$ \displaylines{ \superboxepsillustrate{cour_009b.ps} \cr \tresultat {loi binômiale $\cal B$ (60; 5/6)} \cr }$$ } Les représentations graphiques de ces lois sont données ci-dessous~: % $$ \box \boxone \box \boxtwo $$ La probabilité d'obtenir 10 fois le numéro~$\oldstyle 6$ sur 60 lancers est~: $$ \eqalign { p (X=10) = C_{60}^{10} \left( {1\over 6} \right)^{10} \left( 1 - {1\over 6} \right)^{50} &= {60! \over 10! 50!} \times \left( {1\over 6}\right) ^{10} \times \left( {5\over 6} \right) ^{50} \cr &= {60 \times 59 \times \ldots \times 51 \over 10 \times 9 \times \ldots \times 2 \times 1} \times {5^{50}\over 6^{60}} \approx 0, 137 \cr }$$ La probabilité d'obtenir 50 fois un autre numéro que le numéro~$\oldstyle 6$ sur les 60 lancers est~: $$ \eqalign { p (Y=50) = C_{60}^{50} \left( {5\over 6} \right)^{50} \left( 1 - {5\over 6} \right)^{10} &= {60! \over 50!10! } \times \left( {5\over 6}\right) ^{50} \times \left( {1\over 6} \right) ^{10} \cr &= {60 \times 59 \times \ldots \times 51 \over 10 \times 9 \times \ldots \times 2 \times 1} \times {5^{50}\over 6^{60}} \approx 0, 137 \cr }$$ Ces deux probabilités sont bien sûr égales puisque, comme $X+Y = 60$, on a $Y = 60-X$ et donc $$ p (X = 10) = p (-X = -10) = p (60-X = 60-10) = p (Y=50). $$ Ici, les espérances des variables $X$ et $Y$ sont respectivement $$ E (X) = 60 \times {1 \over 6} = 10 \qquad {\rm et} \qquad E (Y) = 60 \times {5 \over 6} = 50. $$ \endassert