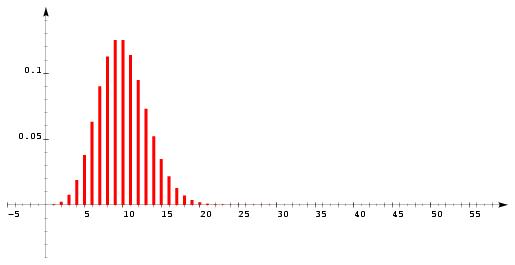
\paragraphe{Loi de Poisson} On dit qu'une variable aléatoire dénombrable $X$, à valeurs dans $\nset$, suit une {\sl loi de Poisson de paramètre $\lambda$} ($\lambda>0$), si et seulement si, pour tout entier naturel $k$, $$\dresultat{ p (X = k) = e^{-\lambda} {\lambda^k \over k!} }$$ On note ${\cal P} (\lambda)$ cette loi, et on montre alors que son espérance, sa variance et son écart-type vérifient $$ \dresultat{E (X) = \lambda} \qquad \qquad \dresultat{V (X) = \lambda} \qquad \qquad \dresultat{\sigma (X) = \sqrt{\lambda}} $$ Dans la pratique, si $n$ est \og grand\fg, $p$ \og voisin\fg\ de $0$ et $np$ pas \og trop grand\fg, on considère en général la loi de Poisson de paramètre $np$ comme une {\sl bonne approximation\/} de la loi binômiale. Plus précisément, si $n \geq 50$, $p\leq 0, 01$ et $np\leq 10$, alors on considère que la loi ${\cal B} (n, p)$ est \og proche\fg\ de la loi ${\cal P} (np)$, ce qui permet d'utiliser la loi de Poisson (à un seul paramètre) plutôt que la loi binômiale (à deux paramètres). Les calculs s'en trouvent alors singulièrement simplifiés\dots On retiendra que, {\bf sous certaines conditions, on peut approcher une loi binômiale par une loi de Poisson ayant la même espérance}. \def \epspath{% $HOME/tex_doc/lycee/database/btsmai/algebre/proba/} \epsfxsize = 80mm $$\displaylines{ \superboxepsillustrate{cour_010.ps} \cr \tresultat {loi de Poisson de paramètre 10} \cr }$$