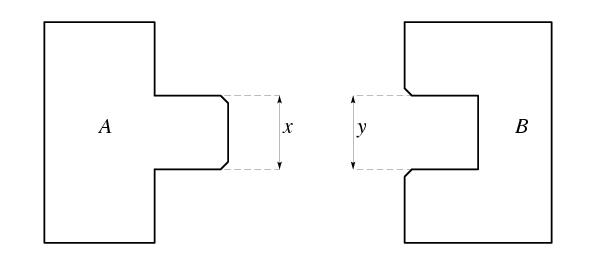
\exo {Ajustements et probabilités, {\rm Bts Mécanique et Automatismes Industriels}, {\sl 1991}} \def \epspath {% $HOME/tex_doc/lycee/database/btsmai/algebre/proba/} \epsfxsize = 140mm Une usine produit des pièces de type $A$ qui doivent s'ajuster dans des pièces de type $B$. $$ \epsillustrate {synt_001.ps} $$ \itemnum Les différentes valeurs prises par la cote $x$ permettent de définir une variable aléatoire $X$ suivant une loi normale de moyenne 20, d'écart-type $0, 04$. \itemitemalph Déterminer la probabilité pour qu'une pièce de type $A$ soit acceptable sachant que sa cote $x$ doit être comprise dans l'intervalle $[19, 92\, ; 20, 08]$. \itemitemalph On suppose maintenant que la proportion de pièces défectueuses de type $A$ réalisées est $0, 05$. On prélève des échantillons de $100$ pièces. Soit $T$ la variable aléatoire prenant pour valeurs le nombre de pièces défectueuses d'un échantillon. \itemitem {} $\bullet $ Quelle est la loi de probabilité de $T$~? On admettra qu'on peut l'assimiler à une loi de Poisson dont on donnera le paramètre. \itemitem {} $\bullet $ Déterminer la probabilité de l'événement~: $\Big[ T<4 \Big] $ \itemnum Les différentes valeurs prises par la cote $y$ permettent de définir une variable aléatoire $Y$ suivant une loi normale de moyenne $20, 1$ et d'écart-type $0, 03$. On suppose d'autre part que les pièces de type $A$ et $B$ peuvent s'assembler si le jeu entre les cotes, $y-x$, est au moins égal à $0, 01$. \item {} On rappelle que si $X$ et $Y$ sont des varables aléatoires suivant des lois normales de moyennes $m_x$ et $m_y$, de variances $V_x$ et $V_y$, alors $Y-X$ suit une loi normale de moyenne $m_y - m_x$ et de variance $V_x + V_y$. \itemitemalph Déterminer la moyenne et l'écart-type de la variable $Y-X$. \itemitemalph Quelle est la probabilité qu'une pièce de type $A$ prise au hasard puisse être introduite dans une pièce de type $B$ également prise au hasard~? \finexo \corrige {} \itemnum Si $X$ suit la loi normale ${\cal N} (20; 0, 04)$, alors la variable $V$ définie par $V = (X-20) / 0, 04$ suit la loi normale centrée réduite ${\cal N} (0, 1)$. \itemalph Une pièce est acceptable si sa cote $x$ vérifie $19, 92 \leq x \leq 20, 08$. D'où $$\eqalign { p ({\rm acceptable}) = p (19, 92 \leq X \leq 20, 08) &= p \left( {19, 92 - 20 \over 0, 04} \leq {X-20 \over 0, 04} \leq {20, 08 - 20 \over 0, 04} \right) \cr &= p (-2 \leq V \leq 2) = 2 \Pi (2) - 1 \cr &= 2 \times 0, 977\, 2 - 1 \qquad {\rm soit} \qquad \dresultat { p ({\rm acceptable}) = 0, 954\, 4} \cr }$$ \itemalph On assimile le prélèvement de 100 pièces à un tirage aléatoire avec remise répété 100~fois. Les expériences sont alors indépendantes, et il n'y a que deux issues observées~: défectueuse ou non, la probabilité d'une issue défectueuse étant de $0, 05$. \item {} On est dans le cadre d'un schéma de Bernouilli et la variable $T$ suit \tresultat {la loi binômiale ${\cal B} (100; 0, 05)$}. On assimile alors cette loi à une loi de Poisson de paramètre $\lambda = 100 \times 0, 05$, soit \mresultat {\lambda = 5}. Dans ce cas, il vient $$\eqalign { P (T < 4) &= p (T=0) + p (T=1) + p (T=2) + p (T=3) \cr &= 0, 007 + 0, 034 + 0, 084 + 0, 140 \qquad {\rm soit} \qquad \dresultat { p (T<4) = 0, 265} \cr }$$ \itemnum La variable $Y$ suit la loi normale ${\cal N} (20, 1; 0, 03)$. Soit $Z$ la variable aléatoire définie par $Z = Y-X$, alors $Z$ suit une loi normale. \itemalph La moyenne de cette loi est $m_z = m_y - m_x = 20, 1 - 20$, soit \mresultat {m_z = 0, 1}. De plus sa variance est $V_z = V_y + V_x = (0, 04)^2 + (0, 03)^2$. Son écart-type est donc $\sigma (Z) = \sqrt {(0, 04)^2 + (0, 03)^2}$, soit \dresultat {\sigma (Z) = 0, 05}. \itemalph Si $Z$ suit la loi normale ${\cal N} (0, 1; 0, 05)$, alors la variable $W$ définie par $W = (Z-0, 1) / 0, 05$ suit la loi normale centrée réduite ${\cal N} (0, 1)$. La probabilité que l'on puisse assembler deux pièces $A$ et $B$ prises au hasard est égale à la probabilité que la variable $Z$ soit supérieure à $0, 01$. D'où le calcul $$\eqalign { p (Z \geq 0, 01) &= p \left( {Z - 0, 1 \over 0, 05} \geq {0, 01 - 0, 1 \over 0, 05} \right) = p (W \geq -1, 8) \cr &= p (W \leq 1, 8) \qquad \hbox {vu la parité de la courbe de la loi ${\cal N} (0, 1)$} \cr &= \Pi (1, 8) \qquad {\rm soit} \qquad \dresultat {p (Z \geq 0, 01) = 0, 964\, 1} \cr }$$ \fincorrige