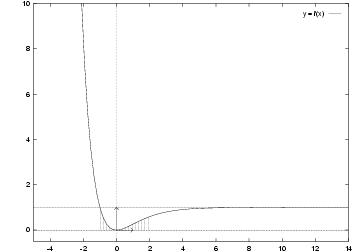
%% format (plain.tex + fichiers de macro) OU (jpv.tex) %% fichiers de macro basejpv.tex %% sujet equation differentielle d'ordre 1 %% date 20-11-97 %% auteur jp vignault \exo{\'Equation différentielle avec une exponentielle} \def \partie#1{% {\bf Partie #1 --}} \partie {A} On considère l'équation différentielle $$ y' + y = 1 - e^{-x} \leqno (E) $$ où l'inconnue $y$ est une fonction de la variable $x$, définie et dérivable sur $\rset$, et où $y'$ est la fonction dérivée de $y$. \itemnum Résoudre l'équation différentielle $$ y' + y = 0 \leqno (E_0) $$ \itemnum Déterminer une fonction numérique $u$ définie et dérivable sur $\rset$ telle que la fonction définie par $$ x \mapsto y_0 = u (x) e^{-x} $$ soit solution de $(E)$ \itemnum Déterminer l'ensemble des solutions de $(E)$. \itemnum Déterminer la solution particulière $g$ de $(E)$ vérifiant la condition initiale $g' (0) = 0$. \clearnumno \bigskip \partie {B} Soit $g$ la fonction définie sur $\rset$ par $$ g (x) = 1 - (x+1) e^{-x} $$ et $C$ sa courbe représentative dans le plan muni d'un repère orthonormal $(O, \vec \imath, \vec \jmath\,)$, unité~: 2~cm. \itemnum Déterminer les limites de $g$ en $-\infty$ et en $+\infty$. En déduire l'existence d'une asymptote $D$ pour $C$. \itemnum \'Etudier les variations de la fonction $g$. \itemnum Construire la droite $D$ et la courbe $C$ après avoir déterminé les coordonnées d'une dizaine de ses points à l'aide d'une calculatrice programmable. \itemitemalphnum \`A l'aide d'une intégration par parties, calculer l'intégrale $$ I = \int_{-1}^2 (x+1) e^{-x} \, dx $$ \itemitemalph En déduire l'aire $\cal A$, en cm$^2$, de la partie du plan limitée par $C$, $D$ et la droite d'équation $x=2$. \itemitemalph Donner un encadrement de $\cal A$ d'amplitude $10^{-2}$. \finexo \corrige{} \itemnum Le cours donne immédiatement que les solutions de l'équation $(E_0)$ sont toutes les fonctions du type $$ \tresultat{$y = k e^{-x}$, où $k \in \rset$} $$ \itemnum On cherche maintenant une solution $g$ de l'équation $(E)$, où $g$ peut s'écrire sous la forme $g (x) = u (x) e^{-x}$ pour une certaine fonction $u$. Guidé par notre expérience (et aussi par un coup d'{\oe}il sur le texte de la partie {\bf B.}), nous essayons dans un premier temps de voir si un polynôme du premier degré peut convenir pour $u$~: \item{} $\bullet$ On pose $$ u (x) = ax+b \qquad {\rm d'où} \qquad u' (x) = a, \qquad g (x) = (ax+b) e^{-x}, \qquad g' (x) = (-ax + a-b) e^{-x}. $$ En calculant $g' + g$, il vient alors $$ g' + g = a e^{-x} $$ On voit que si l'on veut obtenir une solution de $(E)$, il faudra prendre $a=-1$ (et donc $g= -xe^{-x}$), mais cela ne suffira pas. \item{} $\bullet$ Après un peu de réflexion, on s'aperçoit qu'il faut ajouter une constante convenable et que la fonction $g$ définie par $g (x) = 1 - x e^{-x}$ est une solution particulière de l'équation $(E)$. Autrement dit, si on prend pour $u$ la fonction définie par \dresultat{u (x) = e^x - x}, alors la fonction $g$ définie par $g (x) = u (x) e^{-x}$ est une solution particulière de $(E)$ (car $( e^x - x) e^{-x} = 1 - x e^{-x}$). \itemnum L'ensemble des solutions de $(E)$ est obtenu en ajoutant une solution particulière de $(E)$ à la solution générale de $(E_0)$. Ici on obtient donc pour solution de $(E)$ toutes les fonctions $g$ ayant une définition du type $$ \dresultat{g (x) = 1 + (k-x) e^{-x}}, \qquad {\rm où} \quad k \in \rset. $$ \itemnum Si $g$ est une solution de $(E)$, on aura alors $g' (x) = (x-k-1) e^{-x}$, et $g' (0) = -k - 1$. Pour avoir $g' (0) = 0$, il faut donc prendre $k = -1$, d'où la solution cherchée $$ \dresultat{g (x) = 1 - (x+1) e^{-x}}, $$ qui est bien la fonction proposée dans la deuxième partie du problème. \clearnumno \bigskip {\bf B.} On considère la fonction $g$ définie sur $\rset$ par \quad $ g (x) = 1 - (x+1) e^{-x} $ \itemnum On a évidemment $\dresultat{\lim_{x \rightarrow -\infty} g (x) = +\infty}$ puisque $\displaystyle \lim_{x \rightarrow -\infty} e^{-x} = +\infty$. Et on a \dresultat{\lim_{x \rightarrow +\infty} g (x) = 1} puisque $g (x) = 1 - xe^{-x} + e^{-x}$ avec $\displaystyle \lim_{x \rightarrow +\infty} e^{-x} = 0$ et $\displaystyle \lim_{x \rightarrow +\infty} xe^{-x} = 0$ (cf cours). Pour la dernière limite, on peut également partir de l'écriture $g (x) = 1 - (x+1) e^{-x}$ et invoquer le fait que lorsque $x$ tend vers l'infini, l'exponentielle l'emporte sur le polynôme $(x+1)$. \itemnum On a \mresultat{g' (x) = x e^{-x}}, qui est \tresultat{toujours du signe de $x$} puisque l'exponentielle est toujours strictement positive. On obtient alors le tableau de variations suivant~: $$\vbox{ \eightpoint\rm \def \hfq{\hfil \ } \offinterlineskip \halign{ % preamble &\hfq #\hfq \cr $x$& \vrule& $-\infty$&& $0$&& $+\infty$% \cr \noalign{\hrule} $g' (x)$& \vrule height 10pt depth 3pt && $-$& $0$& $+$ \cr \noalign{\hrule} \bbuucenter{$g (x)$}& \vrule& \bbuup{$+\infty$}\hfill& \bbrightddownarrow & \down{$0$}& \bbrightuuparrow & \bbuup{$1$}% \cr }} $$ \def \epspath{% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} $$ \superboxepsillustrate{equ1_010.ps} $$ \itemalphnum Pour calculer l'intégrale $I$, on procède à une intégration par parties en posant $U = (x+1)$ et $V' = e^{-x}$, on a alors $U' = 1$ et $V = -e^{-x}$. Il vient alors $$ I = \int_{-1}^2 (x+1) e^{-x} \, dx = \left[ - (x+1) e^{-x} \right]_{-1}^2 - \int_{-1}^2 -e^{-x} \, dx = -3e^{-2} - \left[ e^{-x} \right]_{-1}^2 = \dresultat{e - 4 e^{-2} = I} $$ \itemalph L'intégrale $I$ est une mesure, en unités d'aire, de $\cal A$. L'unité graphique étant de $2$~cm sur $Ox$ et $2$~cm sur $Oy$, on a ${\cal A} = 4 \times (e - 4 e^{-2})$, soit $$ \dresultat{{\cal A} = \left( 4e - {16 \over e^2} \right) {\rm cm}^2}. $$ \itemalph Un encadrement de $\cal A$ est donc, par exemple $$ \dresultat{0, 70 \leq {\cal A} \leq 0, 71} $$ \fincorrige