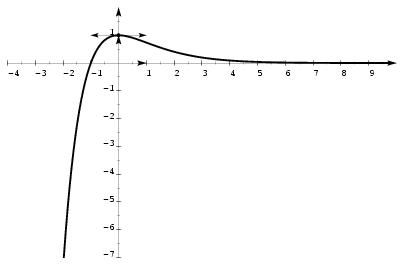
\exo {\'Equation différentielle du premier ordre à coefficients constants} Les deux parties sont indépendantes \medskip {\bf Partie A -} L'objectif de cette partie est la résolution de l'équation différentielle $$ y' + y = e^{-x} \leqno (E) $$ où $y$ est une fonction, définie sur $\rset$, de la variable $x$, et $y'$ la dérivée de $y$. \itemnum Résoudre sur $\rset$ l'équation différentielle $$ y' + y = 0 \leqno (E_0) $$ \itemnum Déterminer le nombre réel $a$ tel que la fonction $g$ définie par $g (x) = ax e^{-x}$ soit solution de $(E)$. \itemnum Donner les solutions de l'équation $(E)$ sur $\rset$. \itemnum Déterminer la fonction $f$, solution de $(E)$, qui vérifie $f (0) = 1$. \clearnumno \medskip {\bf Partie B -} L'objectif de cette partie est l'étude d'une fonction. Soit $f$ la fonction de la variable réelle $x$ définie sur $\rset$ par $$ f (x) = (x+1) e^{-x}. $$ \itemnum Déterminer les limites de $f$ en $+\infty$ et en $-\infty$. \itemnum \'Etudier les variations de la fonction $f$. \itemnum Construire la courbe représentative de la fonction $f$ dans un repère orthogonal $(O, \vec \imath, \vec \jmath\,)$ (unités gra\-phi\-ques~: 1~cm sur $Ox$ et 10~cm sur $Oy$). {\sl Note\/}~: pour les unités graphiques, on pourra utiliser des grands carreaux plutôt que des cm. \finexo \corrige{} \let \partie \llappartie \partie {A} % \vskip -5mm \itemnum D'après le cours, les solutions de $(E_0)$ sont toutes les fonctions $y$ du type $$ \mresultat{y = ke^{-x}, \quad k \in \rset}. $$ \itemnum Si $g$ est la fonction définie par $g (x) = ax e^{-x}$, alors $g' (x) = (-ax + a) e^{-x}$, et on a $g' + g = a e^{-x}$. Pour que $g$ soit solution de l'équation $(E)$, il faut donc prendre $a = 1$. La fonction $g$ définie par \dresultat {g (x) = x e^{-x}} est alors une solution particulière de $(E)$. \itemnum Pour avoir la solution générale de $(E)$, il suffit d'ajouter une solution particulière de $(E)$ à la solution générale de $(E_0)$. Les solutions de $(E)$ sont donc toutes les fonctions $y$ du type $$ \dresultat{y = (x+k) e^{-x}, \quad k \in \rset} $$ \itemnum Si $f$ est une solution de $(E)$, son écriture est de la forme $y = (x+k) e^{-x}$ pour une certaine constante réelle $k$. Comme $f (0) = k$ et que l'on veut $f (0) = 1$, on voit que la seule fonction répondant à la question posée est la fonction $f$ définie par $$ \mresultat{f (x) = (x+1) e^{-x}}. $$ \partie {B} % \vskip -5mm \itemnum En écrivant $f (x) = xe^{-x} + e^{-x}$, on a facilement que \dresultat{\lim_{x \rightarrow +\infty} f (x) = 0} (car $\displaystyle \lim_{-\infty} xe^x = 0$, cf formulaire). \item{} En $-\infty$, la limite n'est pas indéterminée, et on a \dresultat{\lim_{x \rightarrow -\infty} f (x) = -\infty}. \itemnum On a \mresultat{f' (x) = -xe^{-x}}, du signe de $-x$ car l'exponentielle est toujours positive. D'où le tableau de variations et la courbe~: \def \epspath{% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} \epsfxsize = 60 truemm $$\vcenter{ \eightpoint\rm \def \hfq{\hfil \ } \offinterlineskip \halign{ % preamble &\hfq #\hfq \cr $x$& \vrule depth 5pt & $-\infty$&& $0$&& $+\infty$% \cr \noalign{\hrule} $f' (x)$& \vrule height 10pt depth 3pt && $+$& $0$& $-$ \cr \noalign{\hrule} \bbuucenter{$f (x)$}& \vrule& \down{$-\infty$}\hfill& \bbrightuuparrow & \bbuup{$1$}& \bbrightddownarrow & \down{$0$} \cr }} \qquad \vcenter{\superboxepsillustrate{equ1_011.ps}} $$ \fincorrige