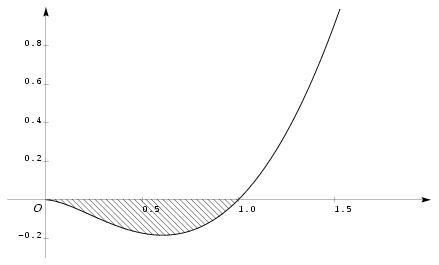
\exo {\' Eqution différentielle, intégration~: un problème de synthèse} On considère, sur $]0, +\infty[$, l'équation différentielle $$ y' - 2 {y\over x} = x \leqno (E) $$ où $y$ représente une fonction de la variable réelle $x$, définie et dérivable sur $]0, +\infty[$, de dérivée première $y'$. \itemitemalphnum Résoudre sur $]0, +\infty[$ l'équation $$ y' - 2 {y\over x} = 0. \leqno (E_0) $$ \itemitemalph Rechercher une solution particulière de $(E)$ sous la forme $$ y (x) = \alpha x^2 \ln x. $$ où $\alpha$ est une constante réelle à déterminer. \itemitemalph Donner la solution générale de $(E)$. \itemitemalph Déterminer la solution de $(E)$ dont la représentation graphique passe par le point $A (1, 0)$. \itemnum On définit sur $]0, +\infty[$ la fonction $f$ par~: $$ f (x) = x^2 \ln x. $$ La représentation graphique de la fonction $f$ dans le plan muni d'un repère orthogonal (unités gra\-phi\-ques~: $32\mm$ sur $Ox$ et $40 \mm$ sur $Oy$) est donnée ci-dessous~: % \def \epspath{% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} % \epsfxsize = 100mm % $$ \superboxepsillustrate{equ1_020.ps} $$ \itemitemalph Calculer $f' (x)$. \itemitemalph \'Etudier les limites de la fonction $f$ en $0$ et en $+\infty$. \itemitemalph \'Etudier les variations de la fonction $f$ et résumer les conclusions dans un tableau. \itemitemalphnum En effectuant une intégration par parties, calculer $$ I (\lambda) = \int_\lambda^1 x^2 \ln x \, dx $$ où $\lambda$ est un réel tel que $0 < \lambda \leq 1$. \itemitemalph Déterminer $ \displaystyle{ \lim_{\lambda \rightarrow 0} I (\lambda) }$. \itemitemalph En déduire l'aire, en $\mm^2$, de la partie du plan hachurée sur la figure ci-dessus. \finexo \corrige{} \itemalphnum Le cours nous dit que les solutions de l'équation $$ y' = {2 \over x} y \leqno (E_0) $$ sont toutes les fonctions $y$ ayant une écriture du type $y (x) = k e^{2 \ln x}$ où $k$ est un réel quelconque, puisque $2 \ln x$ est une primitive de $2 / x$. Cette écriture peut se simplifier en remarquant que $2 \ln x = \ln x^2$, et que $e^{\ln x^2} = x^2$. Ainsi, les solutions de l'équation $(E_0)$ sont toutes les fonctions $y$ ayant une écriture du type \mresultat{y (x) = kx^2} où $k$ est un réel quelconque. \itemalph Posons $y (x) = \alpha x^2 \ln x$, on aura alors $y' (x) = 2 \alpha x \ln x + \alpha x$. Il vient alors $$ y' - {2 \over x} y = 2\alpha x \ln x + \alpha x - 2\alpha x \ln x = \alpha x. $$ Pour que $y$ soit une solution de $(E)$, il faut donc prendre $\alpha = 1$, d'où la solution particulière de $(E)$ cherchée~: \mresultat{y (x) = x^2 \ln x}. \itemalph Pour avoir la solution générale de $(E)$, il suffit d'additionner la sol;ution générale de $(E_0)$ à une solution particulière de $(E)$. En utilisant les deux questions précédentes, on obtient la solution générale de $(E)$ $$\dresultat{ y (x) = x^2 (k + \ln x) \qquad \hbox{ où $k$ est un réel quelconque} }$$ \itemalph Si la représentation graphique de l'une des solutions $f$ de $(E)$ passe par le point $A (1, 0)$, c'est que l'on a $f (1) = 0$. Or, si $y$ est une solution de $(E)$, on a $y (1) = k$ d'après la solution précédente. La solution cherchée est donc la fonction $f$ définie sur $]0, +\infty[$ par \mresultat{f (x) = x^2 \ln x}. \itemnum Le calcul de la fonction dérivée donne $f' (x) = 2x \ln x + x$, soit \mresultat{f' (x) = x (1+2\ln x)}, qui est du signe de $1+2\ln x$ puisque $x>0$. Or $$ 1+2\ln x \geq 0 \quad \Leftrightarrow \quad \ln x \geq -1/2 \quad \Leftrightarrow \quad x \geq e^{-1/2} = 1/\sqrt e, $$ d'où le tableau de variation de la fonction $f$~: {\eightpoint \rm $$\dresultat{ \vcenter{\eightpoint\rm \def \hfq{\hfil \ } \offinterlineskip \halign{ % preamble &\hfq #\hfq \cr $x$& \vrule depth 5pt & & $0$&& $1 / \sqrt e$&& $+\infty$% \cr \noalign{\hrule} $f' (x)$& \vrule height 10pt depth 3pt & \doublevrule && $-$& $0$& $+$ \cr \noalign{\hrule} \bbuucenter{$f (x)$}& \vrule& \doublevrule & \bbuup{$0$}& \bbrightddownarrow & \down{$-1 /2e$}& \bbrightuuparrow & \bbuup{$+\infty$} \cr }}} $$} puisque l'on a $ f \left( {1 \over \sqrt e}\right) = \left( {1 \over \sqrt e}\right)^2 \ln \left( {1 \over \sqrt e}\right) = -{1 \over 2e} $ et $\lim_0 f (x) = 0$ et $\lim_{+\infty} f (x) = +\infty$ d'après le cours de terminale (\og En $0$ ou en $+\infty$, les polynômes l'emportent sur la fonction $\ln$\fg). \itemalphnum En effectuant une intégration par parties où l'on pose $V' = x^2$ et $U = \ln x$, il vient $V = x^3 / 3$ et $U' = 1/x$. D'où $$\eqalign{ \int_\lambda^1 x^2 \ln x \, dx &= \left[ {x^3 \over3} \ln x \right]_\lambda^1 - \int_\lambda^1 {x^2 \over3} \, dx = - {1\over3} \left( \lambda^3 \ln \lambda + {1\over3} \big[ x^3\big]_\lambda^1 \right) \cr &= - {1\over3} \left( \lambda^3 \ln \lambda + {1\over3} (1-\lambda^3) \right) \cr }$$ soit finalement \dresultat{I (\lambda) = -{1\over9} + {\lambda^3 \over3} \Big( {1\over3} - \ln \lambda \Big)}. \itemalph Comme en $0$, le polynôme l'emporte sur la fonction $\ln$, on a \dresultat{\lim_{\lambda \rightarrow 0} I (\lambda) = -{1\over9}}. \itemalph La fonction $f$ étant négative sur l'intervalle $[\lambda, 1]$, l'aire hachurée est donnée, en unité d'aire, par le calcul de $- \int_\lambda^1 f (x) \, dx$. Et comme l'unité d'aire est de $32 \times 40 = 1280 \mm^2$, on en déduit l'aire $\cal A$ cherchée~: $$ \dresultat{{\cal A} = {1280 \over9} \mm^2} \simeq 142, 3 \mm ^2 $$ \fincorrige