Source de equ1

$Fichier TeX$
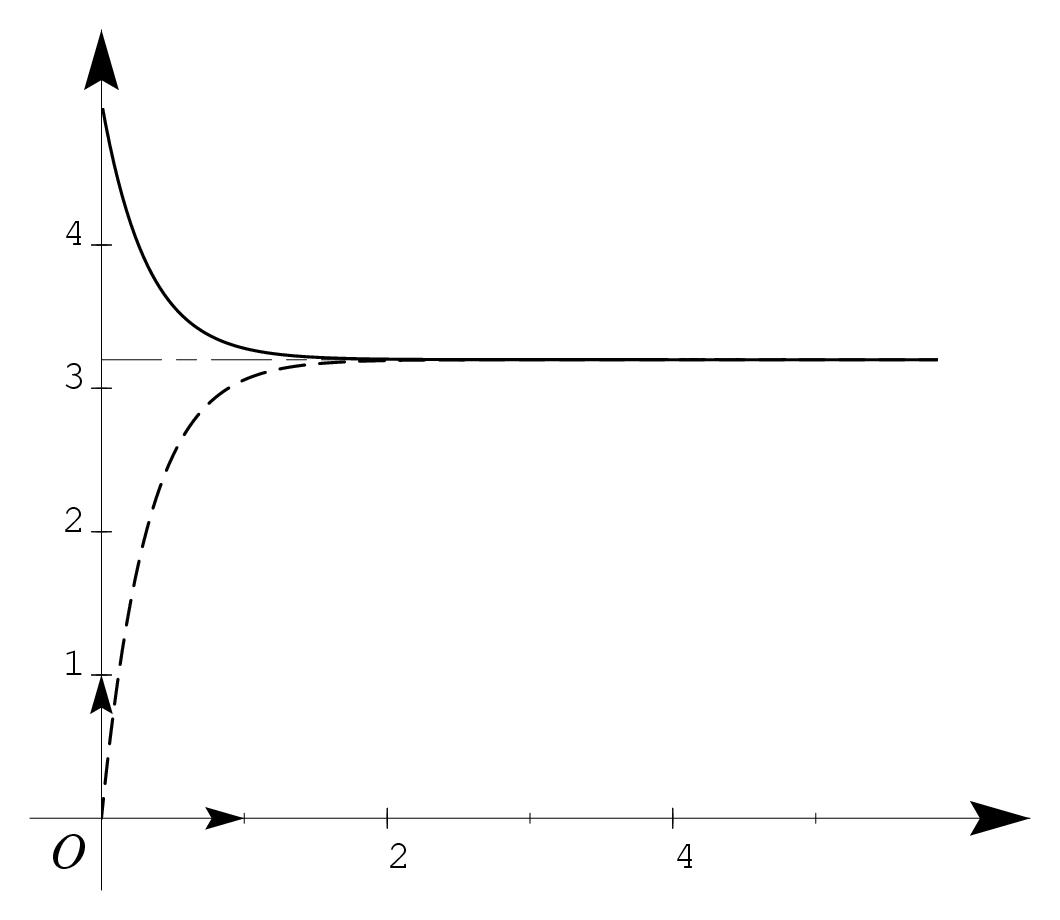
\exo {Le parachute, {\rm Bts Mécanique et Automatismes Industriels}, {\sl 1991}}

La trajectoire suivie par un objet relié à un parachute est un axe
vertical noté $(O, \vec \imath )$.

\` A un instant donné, le vecteur vitesse $\overrightarrow {V}$ de
l'objet est défini par $\overrightarrow {V} (t) = v (t) \vec \imath $
où $v$ est une fonction de la variable réelle positive $t$.

Dans ces conditions de l'expérience, le vecteur $\overrightarrow {R}$
représentant la résistance de l'air est défini par $\overrightarrow
{R} = -k\overrightarrow {V}$ où $k$ est un nombre réel strictement
positif.

On admet que la fonction $v$ vérifie l'équation différentielle
$$
   mv' (t) + k v (t) = mg
\leqno
   (1)
$$
où $m$ est la masse totale de l'objet et du parachute et $g$ le
coefficient de l'accélération de la pesanteur.

\itemitemalphnum Montrer qu'il existe une fonction constante, solution
particulière de $(1)$;

\itemitemalph Montrer que les fonctions solutions de $(1)$ sont définies
pour tout nombre réel positif $t$ par~:
$$
   v (t) = Ce^{-{k\over m} t} + {mg\over k}
$$
où $C$ est une constante réelle dépendant des conditions de l'expérience.

\def \epspath {%
   /home/jp/tex_doc/lycee/database/btsmai/analyse/equadiff/}
\epsfxsize = 60mm
$$
   \epsillustrate {equ1_023a.ps}
$$

\itemnum Dans la suite du problème on prendra $m = 8\kg $, $g =
10$~ms$^{-2}$ et $k = 25$~unités SI.

\itemitemalph Donner la fonction particulière $v_1$ solution de
l'équation différentielle $(1)$ cor\-res\-pon\-dant à une vitesse initiale
$v (0) = v_0$ de $5$~ms$^{-1}$.

\itemitemalph Donner la fonction particulière $v_2$ solution de
l'équation différentielle $(1)$ cor\-res\-pon\-dant à une vitesse initiale
nulle.

\itemitemalph Montrer que les fonctions $v_1$ et $v_2$ ont la même
limite $d$ lorsque $t$ tend vers $+\infty $.

\itemitemalph Donner la solution particulière $v_3$ solution de
l'équation différentielle $(1)$ cor\-res\-pon\-dant à une vitesse initiale
$v (0) = w_0$  de $3, 2$~ms$^{-1}$.

\itemitemalph Tracer soigneusement les courbes $C_1$, $C_2$ et $C_3$
représentant respectivement les fonctions $v_1$, $v_2$ et $v_3$ dans
un repère orthogonal $(O, \vec \imath , \vec \jmath )$, où l'unité
graphique est de 4~cm sur l'axe $Ox$, et 2~cm sur l'axe $Oy$.

\finexo

\corrige {}

\`A résoudre l'équation différentielle 
$$
   mv' + kv = mg.
\leqno
   (1)
$$

\itemalphnum Si $w$ est une fonction constante, solution de
l'équation $(1)$, alors on aura bien sûr \dresultat {w (t) = {mg
\over k}} puisque $w' = 0$.

\itemalph On commence par résoudre l'équation sans second membre $(E_0)$~:
$$
   (E_0) \qquad mv' + kv = 0
      \qquad \Longleftrightarrow \qquad
   v' = - {k \over m}v
$$
dont la solution générale est $v_0 (t) = C e^{-{k\over m}t }$ où $C$
est une constante réelle quelconque. Reste à ajouter une solution
particulière de l'équation $(1)$. On obtient ainsi la solution
générale de l'équation $(1)$~: 
$$
   \dresultat {v (t) = C e^{-{k\over m}t} + {mg \over k} \quad
      \hbox {où $C$ est une constante réelle quelconque}}.
$$

\itemnum Avec les valeurs numériques proposées par l'énoncé,
      l'équation $(1)$ s'écrit 
$$
   \dresultat {(1) : \quad 8v' + 25 v = 80}
      \qquad \hbox {dont la solution générale est} \qquad
   \dresultat {v (t) = C e^{- {25 \over 8} t} + {16 \over 5}, \quad C \in
      \rset }
$$
En particulier, on a \dresultat {v (0) = C + {16 \over 5}}

\itemalph Si $v (0) = 5$, on obtient immédiatement 
$$
   C = 5 - {16 \over 5}
      \qquad {\rm soit} \qquad
   \dresultat {C = {9 \over 5}}
      \qquad {\rm et\ donc} \qquad
   \dresultat {v_1 (t) = {1 \over 5} \left( 9e^{-{25 \over 8} t } + 16\right)}
$$

\itemalph Si $v (0) = 0$, on obtient 
$$
   \dresultat {C = - {16 \over 5}}
      \qquad {\rm et\ donc} \qquad
   \dresultat {v_2 (t) = {16 \over 5} \left( 1 -e^{-{25 \over 8} t } \right)}
$$

\everymath = {\displaystyle }

\itemalph Comme $\lim _{x \to +\infty } e^{-x} = 0$, il est clair que
      l'on a
\dresultat {\lim _{x \to +\infty } v_1 (t) = {16 \over 5} = \lim _{x
\to +\infty } v_2 (t)}.

\itemalph Enfin si $\displaystyle v (0) = {16 \over 5} = 3, 2$, on obtient 
$$
   \dresultat {C = 0}
      \qquad {\rm et\ donc} \qquad
   \dresultat {v_3 (t) = {16 \over 5} = 3, 2}
$$

\def \epspath {%
   /home/jp/tex_doc/lycee/database/btsmai/analyse/equadiff/}
\epsfxsize = 100mm

\itemalph Pour tracer ces courbes, il faut évidemment étudier les
      variations des fonctions $v_1$, $v_2$ et $v_3$. On trouve $v'_1
      (t) = - {45 \over 8} e^{- {25 \over 8} t}$ toujours négatif
      puisque l'exponentielle est toujours positive, et $v'_2 (t) = 10
      e^{- {25 \over 8} t}$ qui est toujours positif. La fonction
      $v_3$ est quand à elle constante. D'où les tableaux de
      variations suivants~:
$$
\dresultat {\vcenter {%
\eightpoint\rm
   \def \hfq{\hfil \ }
   \offinterlineskip
   \halign{
   % preamble
      &\hfq #\hfq
   \cr
      $x$& \vrule depth 5pt 
      & $0$&& $+\infty $%
   \cr
   \noalign{\hrule}
      $v_1' (x)$& \vrule height 10pt depth 3pt 
      && $-$ 
   \cr
   \noalign{\hrule}
      \bbucenter{$v_1 (x)$}& \vrule 
      & \bbup {$5$}& \bbrightdownarrow & \down {$3, 2$}
   \cr
}}}
   \qquad \qquad \qquad 
\dresultat {\vcenter {%
\eightpoint\rm
   \def \hfq{\hfil \ }
   \offinterlineskip
   \halign{
   % preamble
      &\hfq #\hfq
   \cr
      $x$& \vrule depth 5pt 
      & $0$&& $+\infty $%
   \cr
   \noalign{\hrule}
      $v_2' (x)$& \vrule height 10pt depth 3pt 
      && $+$ 
   \cr
   \noalign{\hrule}
      \bbucenter{$v_2 (x)$}& \vrule 
      & \down{$0$}& \bbrightuparrow & \bbup{$3, 2$}
   \cr
}}}
$$
et les courbes~:
$$
   \superboxepsillustrate {equ1_023b.ps}
$$

\fincorrige
— Syracuse — Dernière modification : 30 novembre 2006 (0.08s - 3824218 - 3 décembre 2008)