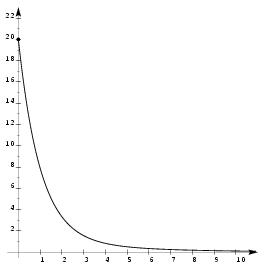
\exo {\' Evolution d'une température en chimie} \centerline {\sl Les questions {\bf 1.} et {\bf 2.} sont indépendantes.} \itemnum On note $y (t)$ la température en degrés Celsius d'une réaction chimique en fonction du temps $t$, $t$ étant exprimé en heures. Après étude, on constate que la température est solution de l'équation différentielle $$ y' + y = e^{-0, 25t} \leqno (E) $$ avec la condition initiale $y (0) = 20$. \itemitemalph Résoudre sur $[0, +\infty [$ l'équation $$ y' + y = 0 \leqno (E_0) $$ \itemitemalph Déterminer le nombre réel $k$ tel que la fonction $g$ définie par $g (t) = k e^{-0, 25t}$ soit une solution particulière de l'équation $(E)$. \itemitemalph En déduire la solution générale de $(E)$. \itemitemalph Déterminer la solution de $(E)$ satisfaisant la condition initiale. \itemnum On considère la fonction $f$ définie sur $[0, +\infty [$ par $$ f (t) = {1\over 3} \left( 56 e^{-t} + 4 e^{-0, 25t}\right) . $$ \itemitemalph \' Etudier la limite de $f$ quand $t$ tend vers $+\infty $. \itemitemalph Déterminer la fonction dérivée de $f$. \itemitemalph \' Etudier le signe de $f' (t)$ pour $t \in [0, +\infty [$. En déduire le tableau de variation de $f$. \itemitemalph Dans le plan rapporté à un repère orthogonal $(O, \vec \imath , \vec \jmath \, )$ (unités graphique~: 2~cm ou 2~grand carreaux pour 1~h sur l'axe des abscisses, et 1~cm ou 1~grand carreau pour 1~degré sur l'axe des ordonnées) représenter graphiquement la fonction $f$. \finexo \corrige {} \itemalphnum Le cours nous donne immédiatement que les solutions de l'équation différentielle $(E_0)$ sont toutes les fonctions $y$ ayant une écriture de la forme $$\dresultat { y (t) = k e^{-t} \qquad \hbox {où $k$ est une constante réelle quelconque} }$$ \itemalph On a $g (t) = k e^{-0, 25t}$, donc \dresultat {g' (t) = -0, 25ke^{-0, 25t}}. Si $g$ est solution de $(E)$, alors on a $$\eqalign { g' + g = e^{-0, 25t} \qquad &{\rm soit} \qquad k e^{-0, 25t} - 0, 25k e^{-0, 25t} = e^{-0, 25t} \cr &{\rm soit} \qquad (1-0, 25)k e^{-0, 25t} = e^{-0, 25t} \cr &{\rm d'où} \qquad {3\over 4}k = 1 \qquad {\rm et} \qquad k = {4\over 3} \cr }$$ Finalement la fonction \dresultat { g (t) = {4\over 3} e^{-0, 25t} } est une solution particulière de $(E)$. \itemalph En additionnant une solution particulière de $(E)$ à la solution générale de $(E_0)$, on obtient la solution générale $y$ de $(E)$~: $$\dresultat { y (t) = {4\over 3} e^{-0, 25t} + k e^{-t} \qquad \hbox {où $k$ est une constante réelle quelconque} }$$ \itemalph Si maintenant la fonction $f$ est l'une de ces solutions vérifiant la condition initiale $f (0) = 20$, alors on a $$ f (t) = {4\over 3} e^{-0, 25t} + k e^{-t} \qquad {\rm et} \qquad f (0) = 20 \qquad {\rm soit} \qquad {4\over 3} + k= 20 \quad \Longrightarrow \quad k = {56\over 3} $$ Finalement, la solution cherchée est la fonction $f$ définie sur $[0, +\infty [$ par $$ \dresultat {f (x) = {4\over 3} e^{-0, 25t} + {56\over 3} e^{-t} = {1\over 3} \left( 4e^{-0, 25t} + 56e^{-t}\right) } $$ \itemalphnum Il vient facilement \dresultat {\lim _{x\to +\infty } f (t) = 0} puisque $\lim _ {+\infty } e^{-t} = \lim _ {+\infty } e^{-0, 25t} = 0$. On en déduit que la courbe représentative de $f$ admet l'axe \tresultat {$Ox$ comme asymptote horizontale}. \itemalph On trouve \dresultat {f' (t) = {1\over 3} \left( -56 e^{-t} - e^{-0, 25t}\right) } \itemalph Et cette dérivée est évidemment \tresultat {toujours négative} puisque, l'exponentielle étant toujours positive, $-56e^{-t}$ et $-e^{-0, 25t}$ seront toujours des nombres négatifs, et leur somme ne pourra qu'être elle-même négative. \def \epspath {% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} \epsfxsize = 80mm \itemalph D'où le tableau de variations de $f$ Et sa courbe représentative~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& 0 && +\infty \cr \noalign {\hrule height 1pt } f' (x)&& & -& \cr \noalign {\hrule height 1pt} \bucenter {$f (x)$}&& \bup {$20$} & \brightdownarrow & \down {$0$} \cr }} } \qquad \qquad \vcenter {\superboxepsillustrate {equ1_024.ps}} $$ \fincorrige