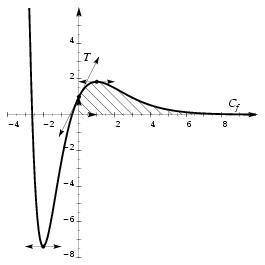
\exo {Un problème de synthèse} {\sl L'objectif de cet exercice est d'étudier la solution $f$ définie sur $\rset $, de la variable $x$, de l'équation différentielle~: $$ y' + y = (2x+3) e^{-x} \leqno (E) $$ vérifiant la condition initiale $f (0) = 1$.} \let \partie \centerpartie \partie {A - Résolution de l'équation différentielle} \itemnum Résoudre sur $\rset $ l'équation différentielle $$ y' + y = 0 \leqno (E_0) $$ \itemnum Vérifier que la fonction $g$ définie sur $\rset $ par $$ g (x) = (x^2 + 3x) e^{-x} $$ est une solution particulière de l'équation différentielle $(E)$. \itemnum Résoudre sur $\rset $ l'équation différentielle $(E)$. \itemnum Déterminer la solution $f$ de cette équation qui vérifie la condition initiale $f (0) = 1$ \partie {B - \' Etude de la solution $f$} Soit $f$ la fonction définie sur $\rset $ par~: $$ f (x) = (x^2 + 3x + 1) e^{-x}. $$ On note $C_f$ sa courbe représentative dans un repère orthonormal $(O, \vec \imath \vec \jmath \, )$ (unité graphique~: 1~cm). \itemnum {\sl \' Etude des variations de la fonction $f$} \itemitemalph Déterminer les limites de $f$ en $+\infty $ et en $-\infty $. \itemitemalph \' Etudier le sens de variation de $f$ et établir son tableau de variation. \itemnum {\sl Position relative de la courbe et de sa tangente au voisinage du point $A$ d'abscisse $0$.} \itemitemalph Déterminer l'équation de la tangente $T$ à la courbe $C_f$ au point $A$ d'abscisse~0. \itemitemalph \' Ecrire le développement limité d'ordre~2 de $f$ au voisinage de~0. En déduire la position relative de $C_f$ et de $T$ au voisinage du point $A$. \itemitemalph Tracer $C_f$ et $T$ dans le repère $(O, \vec \imath \vec \jmath \, )$. \itemnum {\sl Calcul d'une aire} \itemitemalph \` A l'aide d'une intégration par parties, déterminer une primitive de la fonction $h$ définie sur $\rset $ par~: $$ h (x) = (2x+3) e^{-x}. $$ \itemitemalph En se rappelant que la fonction $f$ est une solution de l'équation différentielle $(E)$ et vérifie donc $$ f' (x) + f (x) = (2x+3) e^{-x} $$ et en utilisant le résultat de la question précédente, déterminer une primitive de $f$. \itemitemalph Pour tout nombre réel $\alpha > 0$, on pose~: $$ I (\alpha ) = \int _0^\alpha f (x) \, dx. $$ Calculer $I (\alpha )$. Déterminer la limite de $I (\alpha )$ lorsque $\alpha $ tend vers $+\infty $. Donner une in\-ter\-pré\-ta\-tion graphique de ces résultats. \finexo \corrige {} \let \partie \llappartie \partie {A} \vskip -5mm \itemnum Il vient $$ y' + y = 0 \quad \Longleftrightarrow \quad y' = -y \quad \Longleftrightarrow \quad \tresultat {$y (x) = k e^{-x}$ où $k$ constante réelle quelconque} $$ \itemnum On a $$ g (x) = (x^2 + 3x) e^{-x} \qquad {\rm d'où} \qquad g' (x) = (-x^2 - x + 3) e^{-x}. $$ On vérifie alors facilement que $g' + g = (2x+3) e^{-x}$, ce qui prouve que \tresultat {$g$ est solution particulière de $(E)$}. \itemnum La solution générale de $(E)$ est alors $y (x) = g (x) + k e^{-x}$, soit $$ \tresultat {$y (x) = (x^2 + 3x + k) e^{-x}$ où $k$ constante réelle quelconque} $$ \itemnum La fonction $f$ est solution de $(E)$. Elle s'écrit donc $f (x) = (x^2 + 3x + k) e^{-x}$ pour un certain réel $k$. On aura donc en particulier $f (0) = k$. Sachant que $f(0) = 1$, il vient alors immédiatement \dresultat {f (x) = (x^2 + 3x + 1) e^{-x}} \partie {B} \vskip -5mm \itemalphnum En $+\infty $, il vient $$ \lim _{x\to +\infty } f (x) = \lim _{x\to +\infty } (x^2 + 3x + 1) e^{-x} = \lim _{x\to +\infty } x^2 e^{-x} \qquad {\rm d'où} \qquad \dresultat {\lim _{x\to +\infty } f (x) = 0} $$ puisque $\lim _{x\to +\infty } x^2e^{-x}= 0$ d'après le cours, et que $x^2 + 3x + 1 \sim x^2$ en $+\infty $. \item {} Et en $-\infty $, il vient $$ \lim _{x\to -\infty } f (x) = \lim _{x\to -\infty } (x^2 + 3x + 1) e^{-x} = \lim _{x\to -\infty } x^2 e^{-x} \quad {\rm d'où} \quad \dresultat {\lim _{x\to -\infty } f (x) = +\infty } \quad {\rm puisque} \quad \cases { \lim _{x\to -\infty } x^2 = +\infty \cr \lim _{x\to -\infty } e^{-x} = +\infty \cr } $$ et $x^2 + 3x + 1 \sim x^2$ en $-\infty $. \itemalph On trouve \dresultat {f' (x) = (-x^2 -x +2)e^{-x}}, du signe de $-x^2-x-1$ puisque $e^{-x}$ est toujours positif. \' Etudions le signe de $-x^2-x-1$ avec la méthode du discriminant~: on trouve $\Delta = 9$ et deux racines réelles, $x_1 = -2$ et $x_2 = 1$, et le polynôme est positif (signe de $-a$) entre ces racines. On a donc finalement le tableau de variation suivant~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -\infty && -2&& 1&& +\infty \cr \noalign {\hrule height 1pt} f' (x)&& & - && + && - & \cr \noalign {\hrule height 1pt} \buucenter {$f (x)$}&& \buup {$+\infty $}& \brightddownarrow & \down {$-e^2\approx -7, 39$}& \brightuuparrow & \buup {$5/e \approx 1, 83$}& \brightddownarrow & \down{$0$} \cr }} }$$ \itemalphnum On a $f' (0) = 2$ et $f (0) = 1$ d'où l'équation de la tangente~: \dresultat {T~: y = 2x + 1} \itemalph On sait que $$ e^u = 1 + u + {u^2\over 2} + u^2 \varepsilon (u) \qquad {\rm avec} \qquad \lim _{u\to 0} \varepsilon (u) = 0 $$ d'où $$ e^{-x} = 1 -x + {x^2\over 2} + x^2 \varepsilon (x) \qquad {\rm avec} \qquad \lim _{x\to 0} \varepsilon (x) = 0 $$ et $$ (x^2+3x+1)e^{-x} = (x^2+3x+1) \left( 1 -x + {x^2\over 2}\right) + x^2 \varepsilon (x) \qquad {\rm avec} \qquad \lim _{x\to 0} \varepsilon (x) = 0 $$ soit $$\dresultat { f (x) = 1 + 2x - {3\over 2} x^2 + x^2 \varepsilon (x) \qquad {\rm avec} \qquad \lim _{x\to 0} \varepsilon (x) = 0 }$$ On s'aperçoit alors que la différence entre la courbe et la tangente est $$ f(x) - (2x + 1) = - {3\over 2} x^2 + x^2 \varepsilon (x) \qquad {\rm avec} \qquad \lim _{x\to 0} \varepsilon (x) = 0 $$ qui est toujours négatif pour $x$ au voisinage de $0$. Donc la courbe de $f$ est \tresultat {en dessous de $T$ au voisinage de $0$}. \def \epspath {% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} \itemalph $$ \superboxepsillustrate {equ1_026.ps} $$ \itemalphnum On veut calculer $$ \int (2x+3) e^{-x} \, dx \qquad \hbox {de la forme} \qquad \int U V' \, dx \quad {\rm avec} \quad \cases { U = 2x+3 \cr V' = e^{-x} \cr} \quad {\rm d'où} \quad \cases { U' = 2 \cr V = -e^{-x} \cr} $$ Il vient donc $$ \int h (x) \, dx = \Big[-(2x+3) e^{-x} \Big] - \int -2e^{-x}\, dx = \Big[-(2x+3) e^{-x} \Big] - \Big[2e^{-x} \Big] = \Big[-(2x+3) e^{-x} - 2e^{-x} \Big] $$ d'où une primitive de $h$~: \dresultat {H (x) = -(2x+5) e^{-x}} \itemalph En intégrant la relation $$ f' (x) + f (x) = (2x+3) e^{-x} $$ il vient $$ \int f' (x) + f (x) \, dx = \int (2x+3) e^{-x} \, dx \qquad {\rm soit} \qquad f (x) + \int f (x) \, dx = - (2x+5) e^{-x} $$ Une primitive de $f$ est donc $$ F (x) = \int f (x) \, dx = - (2x+5) e^{-x} - f (x) \qquad {\rm soit} \qquad \dresultat {F (x) = - (x^2+5x+6) e^{-x}} $$ \itemalph On aura donc $$ I (\alpha ) = \int _0^\alpha f (x) \, dx = F (\alpha ) - F (0) \qquad {\rm soit} \qquad \dresultat {I (\alpha ) = - (\alpha ^2+5\alpha +6) e^{-\alpha } + 6} $$ et en reprenant les calculs du {\bf B-1.}{\sl a\/}), on trouve \dresultat {\lim _{\alpha \to +\infty } I (\alpha ) = 6}. Graphiquement, cela signifie que le domaine plan infini limité par la courbe de $f$ et les axes $Ox$ et $Oy$ a une aire finie égale à 6~unités d'aire. \fincorrige