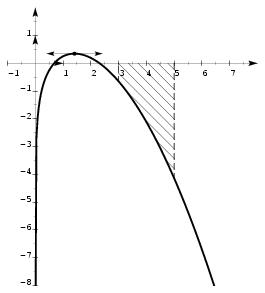
\exo {Un petit problème avec la fonction $\ln $} \let \partie \centerpartie \partie {A -- Résolution d'une équation différentielle} On considère l'équation différentielle $$ xy' - 2y = -2\ln x \leqno (E) $$ où $y$ est une fonction de la variable $x$, définie et dérivable sur $]0, +\infty [$, et $y'$ la fonction dérivée de $y$. \itemnum Résoudre sur $]0, +\infty [$ l'équation différentielle $$ xy' - 2y = 0. \leqno (E_0) $$ \itemnum Vérifier que la fonction $g$ définie sur $]0, +\infty [$ par $$ g (x) = {1\over 2} + \ln x $$ est une solution particulière de $(E)$. \itemnum En déduire la solution générale de $(E)$. \itemnum Déterminer la solution particulière $f$ de $(E)$ prenant la valeur $1/4$ pour $x = 1$. \partie {B -- \' Etude de fonction} On considère la fonction $f$ définie sur $]0, +\infty [$ par $$ f (x) = - {x^2\over 4} + \ln x + {1\over 2}. $$ On admettra que $$ \lim _{x\to +\infty } f (x) = -\infty . $$ \itemitemalphnum Calculer la limite de $f (x)$ lorsque $x$ tend vers~$0$. \itemitemalph \' Etudier les variations de $f$. \itemitem {} ({\sl Autrement dit~: dérivée, signe de la dérivée, tableau de variations\dots }) \itemitemalphnum Montrer que dans l'intervalle $[\sqrt 2, +\infty [$, l'équation $f (x) = 0$ admet une solution unique que l'on notera $\alpha $. \itemitemalph Donner une valeur approchée de $\alpha $ à $10^{-2}$ près par défaut. (Justifier.) \itemnum Construire, dans un repère orthonormal $(O, \vec \imath , \vec \jmath \/)$ d'unité $2$~cm, la portion de la courbe $C_f$ représentative de la fonction $f$ correspondant à $x$ élément de $]0, 5]$. \itemitemalphnum Vérifier que la fonction $H$, définie sur $]0, +\infty [$ par $$ H (x) = x\ln x - x $$ est une primitive de la fonction $\ln $. \itemitemalph Calculer, en cm$^2$, l'aire de la portion de plan comprise entre $C_f$, l'axe des abscisses et les droites d'équation~: $$ x=3 \qquad {\rm et} \qquad x=5. $$ \itemitem {} On donnera une valeur exacte puis une valeur approchée à $10^{-2}$~près. \finexo \corrige {} \let \partie \llappartie \partie {A} % \vskip -5mm \itemnum Il vient $$ xy' - 2y = 0 \qquad \Longleftrightarrow \qquad y' = {2\over x}y $$ Une primitive de $2/x$ étant $2\ln x = \ln (x^2)$, la solution générale de l'équation $(E_0)$ est $$ y (x) = k e^{\ln (x^2)} \qquad {\rm soit} \qquad \dresultat {y (x) = k x^2, \qquad k\in \rset } $$ \itemnum On a $$ g (x) = {1\over 2} + \ln x, \qquad {\rm d'où} \qquad g' (x) = {1\over x}. $$ Il est alors facile de vérifier que $xg' - 2g = -2\ln x$, ce qui prouve que \hfill \break \tresultat {$g$ est une solution particulière de $(E)$}. \itemnum La solution générale de $(E)$ est donc \dresultat {y (x) = kx^2 + {1\over 2} + \ln x, \qquad k\in \rset }. \itemnum Si $f$ est solution de $(E)$, alors $f (1) = k + 1/2$. La condition initiale impose donc $$ k+ {1\over 2} = {1\over 4} \qquad {\rm soit} \qquad k = -{1\over 4} \qquad {\rm d'où} \qquad \dresultat {f (x) = - {x^2\over 4} + {1\over 2} + \ln x}. $$ \partie {B} % \vskip -5 mm \everymath = {\displaystyle } \itemalphnum On a facilement \dresultat {\lim _{x\to 0} f (x) = -\infty } puisque $\lim _{x\to 0} x^2 = 0$ et $\lim _{x\to 0} \ln x = -\infty $. \itemalph On trouve $$ f' (x) = - {x\over 2} + {1\over x} \qquad {\rm soit} \qquad \dresultat {f' (x) = {2-x^2\over 2x}} $$ qui est du signe de $2-x^2$ puisque $2x$ est toujours positif sur l'intervalle considéré. Or $2-x^2$ est un polynôme du second degré qui admet 2~racines réelles ($\sqrt 2$ et $-\sqrt 2$) et qui est positif entre ces racines (signe de $-a$). D'où le tableau de variations de $f$~: $$\dresultat{ \vcenter {\eightpoint \rm \def \hfq{\hfil \ } \offinterlineskip \halign { % preamble &\hfq #\hfq \cr $x$& \vrule depth 5pt & $0$&&& $\sqrt 2$&& $+\infty $% \cr \noalign{\hrule height 1pt} $f' (x)$& \vrule height 10pt depth 3pt & \doublevrule && $+$& $0$& $-$ \cr \noalign {\hrule height 1pt} \bbuucenter{$f (x)$}& \vrule& \doublevrule & \down {$-\infty $}& \bbrightuuparrow & \bbuup {${1\over 2}\ln 2$}& \bbrightddownarrow & \down {$-\infty$} \cr }}} $$ \itemalphnum La fonction $f$ est strictement décroissante sur l'intervalle $[\sqrt 2, +\infty [$ et elle change de signe sur cet intervalle (puisque $f (\sqrt 2)$ est positif alors que $\lim _{+\infty } f (x)$ est négatif). On peut légitimement en conclure que la fonction $f$ \tresultat {s'annule une et une seule fois sur $[\sqrt 2, +\infty [$}. \itemalph Et cette racine $\alpha $ vérifie \dresultat {2, 31 < \alpha < 2, 32} puisque $f (2, 31)$ est positif alors que $f (2, 32)$ est négatif. \def \epspath{% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} \itemnum $$ \superboxepsillustrate {equ1_029.ps} $$ \itemnum Il vient $$ H' (x) = \ln x + {x\over x} - 1 \qquad {\rm soit} \qquad H' (x) = \ln x. $$ donc $H$ est bien \tresultat {une primitive de la fonction $\ln $}. \itemalph La fonction $f$ étant négative sur $[3, 5]$, une mesure en unité d'aire du domaine plan demandé sera~: $$ {\cal A} = - \int _3 ^5 f (x) \, dx = - \int _3 ^5 - {x^2\over 4} + \ln x + {1\over 2}\, dx = - \Big[ - {x^3\over 12} + H (x) + {1\over 2} x\Big] _3 ^5 = \Big[ {x^3\over 12} - x\ln x + {1\over 2} x\Big] _3 ^5 $$ On trouve, après calculs, et en tenant compte du fait qu'une unité d'aire vaut $4~$cm$^2$~: $$\dresultat { {\cal A} = 4 \left( {55\over 6} - 5\ln 5 + 3\ln 3\right) \cm ^2 \approx {17, 66 \cm ^2.} }$$ \fincorrige