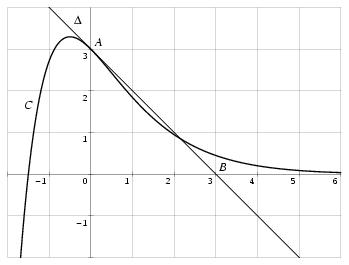
\exo {\' Equation différentielle, {\sl bts mai, session 2003}} \let \partie \centerpartie \centerline {\bf Les trois parties de cet exercice peuvent être traitées de façon indépendante} \partie {A - Résolution d'une équation différentielle} On considère l'équation différentielle $$ y'+y = 2e^{-x} \leqno (E) $$ où $y$ est une fonction de la variable réelle $x$, définie et dérivable sur $\rset $, et $y'$ sa fonction dérivée. \itemnum Déterminer les solutions sur $\rset $ de l'équation différentielle $(E_0)~: y' + y = 0$. \itemnum Soit $h$ la fonction définie sur $\rset $ par $h (x) = 2xe^{-x}$. \item {} Démontrer que la fonction $h$ est une solution particulière de l'équation différentielle $(E)$. \itemnum En déduire l'ensemble des solutions de l'équation différentielle $(E)$. \itemnum Déterminer la solution $f$ de l'équation différentielle $(E)$ dont la courbe représentative, dans un repère orthonormal, passe par le point de coordonnées $(0, 3)$. \partie {B - \' Etude d'une fonction} \itemnum La courbe $C$ ci-dessous représente dans un repère orthonormal $(O, \vec \imath , \vec \jmath \,)$ une fonction $f$ définie sur $\rset $ par $f (x) = (ax+b)e^{-x}$ où $a$ et $b$ sont des nombres réels. \item {} La droite $\Delta $ est la tangente à la courbe $C$ au point $A$ d'abscisse $0$. Cette tangente passe par le point $B$ de coordonnées $(3, 0)$. \def \epspath {% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} $$ \epsillustrate {equ1_030.ps} $$ \itemitemalph Déterminer graphiquement $f (0)$. \itemitemalph Déterminer, graphiquement ou par le calcul, $f' (0)$. \itemitemalph Déterminer les valeurs des nombres réels $a$ et $b$. {\bf Dans la suite, on admet que $f$ est définie sur $\rset $ par $$ f (x) = (2x+3)e^{-x}. $$} \itemitemalphnum Démontrer que, pour tout $x$ de $\rset $, $f' (x) = (-2x-1) e^{-x}$; \itemitemalph Résoudre dans $\rset $ l'inéquation $f' (x) \geq 0$; \itemitemalph En déduire le sens de variation de $f$ sur $\rset $. (On ne cherchera pas les limites en $-\infty $ et en $+\infty $.) \itemitemalphnum Déterminer le développement limité, à l'ordre 2, au voisinage de $0$, de la fonction $x\mapsto e^{-x}$. \itemitemalph Démontrer que le développement limité, à l'ordre 2, au voisinage de $0$, de la fonction $f$ est~: $$ f (x) = 3 - x -{1\over 2}x^2 + x^2 \varepsilon (x) \qquad {\rm avec} \qquad \lim _{x\to 0} \varepsilon (x) = 0. $$ \partie {C - Calcul intégral} \itemnum La fonction $f$ définie dans la partie {\bf B} est une solution de l'équation différentielle $(E)$ de la partie {\bf A}. Donc, pour tout $x$ de $\rset $, $$ f (x) = -f' (x) + 2e^{-x}. $$ En déduire une primitive $F$ de $f$ sur $\rset $. \itemnum On note $\displaystyle { I = \int _{0} ^{1/2} f (x) \, dx }$. \itemitemalph Démontrer que $I = 5 - 6e^{-1/2}$. \itemitemalph Donner une valeur approchée arrondie à $10^{-3}$ de $I$. \itemnum On note $\displaystyle { J = \int _{0} ^{1/2} \left( 3-x- {1\over 2}x^2\right) \, dx }$. \itemitemalph Démontrer que $J = 65/48$. \itemitemalph Donner une valeur approchée arrondie à $10^{-3}$ de $J$. \itemitemalph Vérifier que les valeurs approchées obtenues ci-dessus pour $I$ et $J$ diffèrent de moins de $10^{-2}$. \finexo \corrige \let \partie \llappartie \partie {A} \vskip -5mm \itemnum On reconnaît une équation du type $y' = a y$ avec $a = -1$. Une primitive de $a$ est $A = -x$, et la solution générale de $(E_0)$ est donc \dresultat {y_0 (x) = k e^{-x}} où $k$ est une constante réelle quelconque. \itemnum On a $h (x) = 2xe^{-x}$, donc $h' (x) = (2-2x) e^{-x}$, et on vérifie que l'on a bien $h + h' = 2e^{-x}$, ce qui prouve que \tresultat {$h (x) = 2xe^{-x}$ est une solution particulière de $(E)$}. \itemnum La solution générale de $(E)$ est donc \tresultat {$y (x) = (2x + k) e^{-x}$} où $k$ est une constante réelle quelconque. \itemnum Si la courbe représentative de $f$ passe par le point $(0; 3)$, c'est donc que l'on a $f (0) = 3$. On en déduit que $k=3$, et par suite que \dresultat {f (x) = (2x+3) e^{-x}}. \partie {B} \vskip -5mm \itemalphnum On a bien sûr \dresultat {f (0) = 3}, \quad \alph \quad et on a \dresultat {f' (0) = -1} puisque ce nombre représente le coefficient directeur de la tangente à la courbe de $f$ au point d'abscisse~$0$. \itemalph La condition $f (0) = b = 3$ nous donne immédiatement $b$. Et comme $f' (x) = (a - ax - b)e^{-x}$, il vient $f' (0) = a - b = 3$, et par suite $a=2$. On a donc finalement \dresultat {(a, b) = (2, 3)} et \dresultat {f (x) = (2x + 3) e^{-x}}. \itemalphnum On a facilement \dresultat {f' (x) = (-2x-1)e^{-x}}, qui est du signe de $-2x-1$ puisque $e^{-x}$ est toujours strictement positif. D'où le tableau de variation de $f$~: $$\dresultat {\vcenter { \eightpoint \rm \def \cc#1{\hfill \ #1 \hfill } \offinterlineskip \halign { %% preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -\infty && -1/2&& +\infty \cr \noalign {\hrule } \bbucenter {$f (x)$}&& & \brightuuparrow & \buup {$2\sqrt e$}& \brightddownarrow & \cr }}} \qquad \qquad f \left ( -{1\over 2}\right) = 2e^{1/2} = 2\sqrt e $$ \itemalphnum Connaissant le développement limité de $e^t$ en $0$, on en déduit facilement $$\dresultat { e^{-x} = 1 - x + {x^2 \over 2} + x^2 \varepsilon (x) \qquad {\rm avec} \qquad \hbox {$\displaystyle \lim _{x\to 0} \varepsilon (x) = 0$} }$$ \itemalph Et le produit de ce DL par le polynôme $(2x+3)$ nous donne $$\displaylines { (2x+3) e^{-x} = (2x+3) \left( 1 - x + {x^2 \over 2} \right) + x^2 \varepsilon (x) = 3 + 2x - 3x + {3\over 2} x^2 - 2x^2 + x^2 \varepsilon (x) \cr {\rm d'où} \qquad \dresultat { f (x) = 3 - x -{1\over 2}x^2 + x^2 \varepsilon (x) \qquad {\rm avec} \qquad \lim _{x\to 0} \varepsilon (x) = 0. } \cr }$$ \partie {C} \vskip -5mm \itemnum Il vient $$\displaylines { f (x) = -f' (x) + 2e^{-x} \quad \Longrightarrow \quad \int f (x) \, dx = -\int f' (x) \, dx + \int 2e^{-x} \, dx \cr \qquad {\rm soit} \qquad \int f (x) \, dx = -f (x) -2e^{-x} \cr } $$ d'où une primitive de $f$~: \dresultat {F (x) = -f (x) - 2e^{-x} = (-2x-5)e^{-x}} \itemnum Le calcul de l'intégrale $I$ donne alors $$ I = \int _{0} ^{1/2} f (x) \, dx = F \left( {1\over 2}\right) - F (O) \qquad {\rm soit} \qquad \dresultat {I = -6e^{1/2} + 5 \approx 1, 361} $$ \itemnum Pour $J$, il vient $$ J = \int _{0} ^{1/2} \left( 3-x- {1\over 2}x^2\right) \, dx = \Big[ 3x - {x^2\over 2} - {1\over 6}x^3\Big] _{0} ^{1/2} \qquad {\rm soit} \qquad \dresultat {J = {65\over 48} \approx 1, 354} $$ Et la différence \tresultat {$J-I \approx -6, 649 \cdot 10^{-3}$ est bien inférieure à $10^{-2}$}. \fincorrige