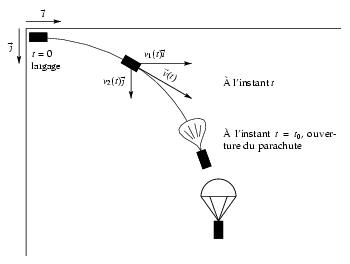
\exo {Largage d'un container, \sl bts mai, session 1994} On lance un container à partir d'un avion. On cherche à déterminer l'instant où la norme de la vitesse est minimale pour pouvoir déclencher l'ouverture du parachute. L'unité de temps est la seconde, l'unité de longueur est le mètre. Le centre de gravité $G$ est repéré para rapport au repère orthonormal $(O, \vec \imath , \vec \jmath )$. L'axe $(O, \vec \jmath )$ est dirigé vers le sol. \` A chaque instant $t$, le point $G$ admet un vecteur vitesse $\vec v (t)$ de coordonnées $v_1 (t)$ et $v_2 (t)$ où $v_1$ et $v_2$ sont des fonctions du temps définies sur $[0; +\infty [$. \def \epspath{% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} $$ \superboxepsillustrate {equ1_031.ps} $$ Sachant que le container est soumis à son poids et à la résistance de l'air, on établit que~: $\bullet $ la fonction $v_1$ vérifie l'équation différentielle $$ v' + 0, 2 v = 0 $$ $\bullet $ la fonction $v_2$ vérifie l'équation différentielle $$ v' + 0, 2 v = 9, 8. $$ \itemitemalphnum Résoudre l'équation différentielle $$ v' + 0, 2 v = 0. $$ \itemitemalph Sachant de plus que pour $t = 0$, on a $v_1 (0) = 100$, déterminer $v_1 (t)$. \itemitemalphnum Résoudre l'équation différentielle $$ v' + 0, 2 v = 9, 8. $$ \itemitemalph Sachant de plus que pour $t = 0$, on a $v_2 (0) = 0$, déterminer $v_2 (t)$. \itemitemalphnum Sachant que la norme du vecteur $\vec v (t)$, notée $\Vert \vec v (t)\Vert $, vérifie $$ \Vert \vec v (t)\Vert ^2 = (v_1 (t))^2 + (v_2 (t))^2, $$ démontrer que l'on a~: $$ \Vert \vec v (t)\Vert ^2 = 12\, 401 e^{-0, 4t} - 4\, 802 e^{-0, 2t} + 2\,401. $$ \item {} Afin de simplifier les calculs, on remplace l'étude de $\Vert \vec v (t)\Vert ^2$ par celle de $f (t)$ où la fonction $f$ est définie sur $[0; +\infty [$ par $$ f (t) = 12\, 400 e^{-0, 4t} - 4\, 800 e^{-0, 2t} + 2\,400 = 400 \left( 31 e^{-0, 4t} - 12 e^{-0, 2t} + 6\right). $$ \itemitemalph Calculer $f (0)$. Déterminer $\displaystyle \lim _{x\to +\infty } f (t) $. \itemitemalph \' Etudier les variations de la fonction $f$. \itemitemalph En déduire les variations de la fonction qui à $t\in [0; +\infty [$, associe $h (t) = \sqrt {f (t)}$. \itemitemalph Tracer dans un repère orthogonal ($1\cm $ en abscisse représente $1$ seconde, $1\cm $ en ordonnée représente $10$ mètres par seconde) a courbe représentative de $h$. \itemitemalph En déduire à $10^{-2}$ près par défaut l'instant $t_0$ pour lequel $h (t)$ est minimum. \itemitem {} Déterminer alors ce minimum à $10^{-2}$ près par défaut. \finexo