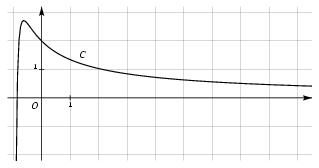
\exo {{\sl bts mai, session 2005}} \def \epspath { $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} \let \partie \centerpartie \centerline {\bf Les trois parties de cet exercice peuvent être traitées de façon indépendante.} \partie {A -- Résolution d'une équation différentielle} On considère l'équation différentielle $(E)$~: $$ (1+x) y' + y = {1\over 1+x}, $$ où $y$ est une fonction de la variable réelle $x$, définie et dérivable sur $]-1; +\infty [$ et $y'$ sa fonction dérivée. \itemnum Démontrer que les solutions sur $]-1; +\infty [$ de l'équation différentielle $(E_0)$~: $$ (1+x) y' + y = 0 $$ sont les fonctions définie par $$ h (x) = {k\over x+1}, \qquad \hbox {où $k$ est une constante réelle quelconque} $$ \itemnum Soit $g$ la fonction définie sur $]-1; +\infty [$ par $$ g (x) = {\ln (1+x)\over 1+x}. $$ Démontrer que la fonction $g$ est une solution particulière de l'équation différentielle $(E)$. \itemnum En déduire l'ensemble des solutions de l'équation différentielle $(E)$. \itemnum Déterminer la solution $f$ de l'équation différentielle $(E)$ qui vérifie la condition initiale $f (0) = 2$. \partie {B -- \' Etude d'une fonction} Soit $f$ la fonction définie sur $]-1; +\infty [$ par $$ f (x) = {2+\ln (1+x) \over 1+x}. $$ Sa courbe représentative $C$, dans un repère orthonormal où l'unité graphique est $1$~cm, est donnée ci-dessous~: $$ \epsillustrate {equ1_034.ps} $$ \itemnum On admet que $\displaystyle {\lim _{x\to -1} f (x) = -\infty }$ et que $\displaystyle {\lim _{x\to +\infty } f (x) = 0}$. Que peut-on en déduire pour la courbe $C$~? \itemitemalphnum Démontrer que, pour tout $x$ de $]-1; +\infty [$, $$ f' (x) = {-1-\ln (1+x)\over (1+x)^2}. $$ \itemitemalph Résoudre dans $]-1; +\infty [$ l'inéquation $$ -1 - \ln (1+x) \geq 0. $$ En déduire le signe de $f' (x)$ lorsque $x$ varie dans $]-1; +\infty [$. \itemitemalph \' Etablir le tableau de variation de $f$. \itemnum Un logiciel de calcul formel donne le développement limité, à l'ordre $2$, au voisinage de $0$, de la fonction $f$~: $$ f (x) = 2 - x + {1\over 2} x^2 + x^2 \varepsilon (x) \qquad {\rm avec} \qquad \lim _{x\to 0} \varepsilon (x) = 0. $$ {\sl Ce résultat, admis, n'a pas à être démontré.} \itemitemalph En déduire une équation de la tangente $T$ à la courbe $C$ au point d'abscisse~$0$. \itemitemalph \' Etudier la position relative de $C$ et $T$ au voisinage de leur point d'abscisse $0$. \partie {C - Calcul intégral} \itemnum Déterminer la dérivée de la fonction $G$ définie sur $]-1; +\infty [$ par $$ G (x) = {1\over 2} \big( \ln (1+x)\big) ^2. $$ \itemnum En déduire qu'une primitive de la fonction $f$ sur $]-1; +\infty [$ est définie par $$ F (x) = 2\ln (1+x) + {1\over 2} \big( \ln (1+x)\big) ^2. $$ \itemitemalphnum On note $$ I = \int _0^2 f (x) \, dx. $$ Démontrer que $$ I = {1\over 2} (\ln 3)^2 + \ln 3. $$ \itemitemalph Donner la valeur approchée arrondie à $10^{-2}$ de $I$. \itemitemalph Donner une interprétation graphique du résultat obtenu au {\sl b\/}). \finexo \corrige \let \partie \llappartie \partie {A} % \vskip -5mm \itemnum Il vient $$ (1+x) y' + y = 0 \quad \Longleftrightarrow \quad y' = - {1\over 1+x} y $$ Cette équation est de la forme $y' = a (x) y$ avec $a (x) = - {1\over 1+x}$, et une primitive de $a$ est $A (x) = -\ln (1+x)$. On en déduit que la solution générale de $(E_0)$ est $$ y (x) = ke^{-\ln (1+x)} = ke^{\ln \left( (1+x)^{-1}\right) } \quad {\rm soit} \quad \dresultat {y (x) = {k\over 1+x}} \qquad \hbox {où $k$ est une constante réelle quelconque}. $$ \itemnum Il vient~: $$ g (x) = {\ln (1+x)\over 1+x} \qquad {\rm d'où} \qquad g' (x) = {{1\over 1+x}\times (1+x) - \ln (1+x)\over (1+x)^2} \qquad {\rm soit} \qquad g' (x) = {1 - \ln (1+x)\over (1+x)^2}. $$ On a alors $$\eqalign { (1+x)g' + g &= (1+x) {1 - \ln (1+x)\over (1+x)^2} + {\ln (1+x)\over 1+x} \cr &= {1 - \ln (1+x)\over (1+x)} + {\ln (1+x)\over 1+x} = {1\over 1+x} \cr }$$ ce qui prouve que \tresultat {$\displaystyle {g (x) = {\ln (1+x)\over 1+x}}$ est une solution particulière de l'équation $(E)$} \itemnum La solution générale de $(E)$ est donc \dresultat {y (x) = {k + \ln (1+x)\over 1+x}} où $k$ est une constante réelle quelconque. \itemnum Comme $y (0) = k$, la condition initiale impose $k = 2$, d'où la fonction cherchée~: \dresultat {f (x) = {2 + \ln (1+x)\over 1+x}}. \partie {B} % \vskip -5.5mm \itemnum On a $\displaystyle {\lim _{x\to -1} f (x) = -\infty }$, donc \tresultat {la droite $x = -1$ est une asymptote verticale} de la courbe $C$. Et on a $\displaystyle {\lim _{x\to +\infty } f (x) = 0}$, donc \tresultat {la droite $y = 0$ est une asymptote horizontale} de la courbe $C$. \itemalphnum En utilisant la formule de la dérivée d'un quotient (voir partie A), on obtient bien \dresultat {f' (x) = {-1-\ln (1+x)\over (1+x)^2}}. \itemalph Il vient $$ -1 - \ln (1+x) \geq 0 \quad \Longleftrightarrow \quad -1 \geq \ln (1+x) \quad \Longleftrightarrow \quad e^{-1} \geq 1+x \quad \Longleftrightarrow \quad e^{-1} -1 \geq x $$ d'où l'ensemble des solutions de l'inéquation~: \dresultat {S = \left]-1; e^{-1} - 1\right] } \itemalph D'où le tableau de variations $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -1 &&& e^{-1} - 1&& +\infty \cr \noalign {\hrule height 1pt} -1 - \ln (1+x)&&\doublevrule &&+& 0& -& \cr \noalign {\hrule } (1+x)^2&& &&+&\tv & +& \cr \noalign {\hrule height 1pt} f' (x)&&\doublevrule & &+& 0& -& \cr \noalign {\hrule height 1pt} \buucenter {$f (x)$}&&\doublevrule & \down {$-\infty $}& \brightuuparrow & \buup {$1/e$}& \brightddownarrow & \down{$0$} \cr }} }$$ \itemalphnum L'équation de la tangente, c'est le DL d'ordre $1$. D'où l'équation demandée~: \dresultat {T~: y = 2-x}. \itemalph Au voisinage de $0$, la différence entre la courbe $C$ et la tangente $T$ est donnée par l'expression $$ 2 - x + {1\over 2} x^2 - (2 - x) = {1\over 2} x^2. $$ Cette expression est évidemment toujours positive, ce qui prouve qu'au voisinage de $0$, \tresultat {$C$ est au dessus de $T$}. \partie {C} % \vskip -5mm \itemnum La fonction $G$ est de la forme $ku^2$ où $k$ est une constante réelle. Sa dérivée est donc $G' = 2ku'u$, ce qui donne $$ G' (x) = 2\times {1\over 2} \times {1\over 1+x} \times \ln (1+x) \qquad {\rm soit} \qquad \dresultat {G' (x) = {\ln (1+x)\over (1+x)}}. $$ \itemalph Comme $2\ln (1+x)$ est une primitive de $2\over 1+x$, il est clair que $$ \tresultat {$\displaystyle {F (x) = 2\ln (1+x) + {1\over 2} \big( \ln (1+x)\big) ^2}$ est une primitive de $f$}. $$ \itemalph \alph \quad Il vient $$\eqalign { I = \int _0^2 f (x) \, dx = \Big[ F (x)\Big] _0^2 &= \left( 2\ln (1+2) + {1\over 2} \big( \ln (1+2)\big) ^2\right) - \left( 2\ln (1+0) + {1\over 2} \big( \ln (1+0)\big) ^2\right) \cr &= \dresultat {2\ln 3 + {1\over 2}\big (\ln 3\big)^2 = I\approx 2, 80}. }$$ \itemalph Ce résultat correspond, en unités d'aire à \tresultat {l'aire du domaine plan limité par $C$, $Ox$, $Oy$ et la droite $x = 2$} \def \epspath { $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} $$ \epsillustrate {equ1_034a.ps} $$ \fincorrige