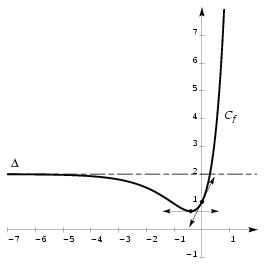
\exo {Le second membre est constant} \let \partie \centerpartie \partie {A} On considère l'équation différentielle $$ y'' - 3y' + 2y = 4. \leqno (E) $$ \itemitemalphnum Résoudre l'équation différentielle $$ y'' - 3y' + 2y = 0. $$ \itemitemalph Déterminer une solution particulière de $(E)$. \itemitemalph En déduire la solution générale de $(E)$. \itemnum Déterminer la solution particulière de $(E)$ vérifiant les 2~conditions~: $$ f (0) = 1 \qquad {\rm et} \qquad f' (0) = 2. $$ \partie {B} Dans un repère orthonormal $(O, \vec \imath, \vec \jmath\,)$ d'unité 4~cm (ou 4~grands carreaux), on considère $C_f$, la courbe représentative de la fonction $f$ définie sur $\rset$ par $$ f (x) = 2 + 3e^{2x} - 4e^x. $$ \itemnum \'Etudier le sens de variation de la fonction $f$. \itemitemalphnum Déterminer la limite de $f$ en $+\infty$ (on pourra mettre $e^{2x}$ en facteur dans $f (x)$). \itemitemalph Montrer que la droite $\Delta$ d'équation $y = 2$, est asymptote à $C_f$. \'Etudier les positions relatives de $C_f$ et $\Delta $. \itemitemalph On note $T$ la droite tangente à $C_f$ au point d'abscisse~0. Calculer le coefficient directeur de $T$. \itemnum Sur le même graphique, tracer les courbes $\Delta$, $T$ et $C_f$. \finexo \corrige {} \let \partie \llappartie \partie {A} % \alphnum \ L'équation caractéristique associée à l'équation sans second membre $(E_0)$ est $$ r^2 - 3r + 2 = 0. $$ Cette dernière équation admettant les 2~solutions réelles $r_1 = 1$ et $r_2 = 2$, on en déduit que la solution générale de $(E_0)$ est la fonction $y$ définie par $$ \dresultat {y (x) = A e^{2x} + B e^x} \qquad \hbox {où $A$ et $B$ contantes réelles quelconques} $$ \alph \ Cherchons une solution particulière de $(E)$ sous la forme d'une fonction constante $g$ définie pour tout réel $x$ par $g (x) = a$, où $a$ est une constante réelle à déterminer. On a alors $g' (x) = g '' (x) = 0$ pour tout $x$. Or l'hypothèse \og $g$ solution de $(E)$\fg \ impose la condition $$ g'' - 3g' + 2g = 4 \qquad {\rm soit} \qquad 2a = 4 $$ On en déduit que la fonction constante $g$ définie pour tout réel $x$ par \dresultat {g (x) = 2} est une solution particulière de l'équation $(E)$. \alph \ Pour obtenir la solution générale de $(E)$, il suffit d'additionner la solution générale de $(E_0)$ à une solution particulière de $(E)$. On en déduit la solution générale de $(E)$~: $$ \dresultat {y (x) = 2 + Ae^{2x} + B e^x} \qquad \hbox {où $A$ et $B$ constantes réelles quelconques} $$ \num \ Si $f$ est une solution de $(E)$, on aura donc $ f' (x) = 2Ae^{2x} + B e^x $, et les conditions initiales $f (0) = 1$ et $f' (0) = 2$ vont alors imposer les relations $$ 2+A+B = 1 \qquad {\rm et} \qquad 2A + B = 2. $$ De ces relations, on déduit $(A, B) = (3, -4)$. D'où la seule solution de $(E)$ vérifiant les 2~conditions initiales~: $$ \dresultat {f (x) = 2 +3e^{2x} - 4e^x} $$ \partie {B} % \num \ Le calcul de la dérivée $f'$ donne $f' (x) = 6e^{2x} - 4e^x$, soit \dresultat {f' (x) = 2e^x \times (3e^x - 2)}. Cette dérivée est du signe de $3e^x - 2$ puisque $2e^x$ est toujours positif. Or $$ 3e^x - 2 \geq 0 \qquad \Longleftrightarrow \qquad e^x \geq {2\over 3} \qquad \Longleftrightarrow \qquad x \geq \ln \left( {2\over 3} \right) = \ln 2 - \ln 3 $$ On en déduit \tresultat {$f$ décroissante sur $]-\infty , \ln 2 - \ln 3]$}, et \tresultat {croissante sinon} \alphnum \ Pour la limite de $f$ en $+\infty $, il vient $$ \lim _{x\to +\infty } f (x) = \lim _{x\to +\infty } e^{2x} \times \big( 2e^{-2x} + 3 - 4 e^{-x}\big) \qquad {\rm soit} \qquad \dresultat {\lim _{x\to +\infty } f (x) = +\infty } $$ puisque $\displaystyle { \lim _{x\to +\infty } e^{-x} = \lim _{x\to +\infty } e^{-2x} = 0 }$ et $\displaystyle { \lim _{x\to +\infty } e^{2x} = +\infty }$ \alph \ Pour ce qui est de $-\infty $, on a $$ \lim _{x\to -\infty } \big( f (x) - 2\big) = \lim _{x\to -\infty } 3e^{2x} - 4e^x = 0 $$ puisque $\displaystyle { \lim _{x\to -\infty } e^{2x} = \lim _{x\to -\infty } e^{x} = 0 }$. On en déduit que $$ \tresultat {la droite d'équation $y=2$ est asymptote en $-\infty $ à la courbe de $f$}. $$ Pour étudier les positions relatives de $C_f$ et $\Delta $, il faut étudier le signe de leur diférence. Or on a $$ f (x) - 2 = 3e^{2x} - 4 e^x = e^x \times \big( 3e^x - 4\big) $$ qui est du signe de $3e^x -4$ puisque $e^x$ est toujours positif. En procédant de la même manière que pour l'étude du signe de la dérivée $f'$, on trouve les résultats suivant~: $$\dresultat { \vcenter{\offinterlineskip \halign{ % preamble & \cc {$#$}& #& $#$ & \cc {$#$}& \cc {$#$}& \cc {$#$}& \cc {$#$}& $#$ \cr x& \tv & \, -\infty && \ln \left( {4\over 3}\right) && +\infty \cr \noalign{\hrule} f (x) - 2 & \tv && - & 0 & + & \cr \noalign{\hrule} \tvi height 15pt depth 10pt \hbox {positions relatives}& \tv && \matrix{C_f {\rm \ au}\cr {\rm dessous\ de\ } \Delta }& \tv & \matrix{C_f {\rm \ au}\cr {\rm dessus\ de\ } \Delta } \cr }} }$$ \alph \ Par définition de la fonction dérivée $f'$, le coefficient directeur de la tangente $T$ est \dresultat {f' (0) = 2} \def \epspath {% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} \num \ En résumé, le tableau de variation de la fonction $f$ est le suivant~: $$\vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -\infty && \ln {2\over 3}&& +\infty \cr \noalign {\hrule height 1pt } f' (x)&& &-& 0& + \cr \noalign {\hrule height 1pt} \buucenter {$f (x)$}&& \buup {$2$}& \brightddownarrow & \down{$2/3$}& \brightuuparrow & \buup {$+\infty $} \cr }} $$ et voici sa courbe représentative~: \epsfxsize 80mm $$ \superboxepsillustrate {equ2_004.ps} $$ \fincorrige