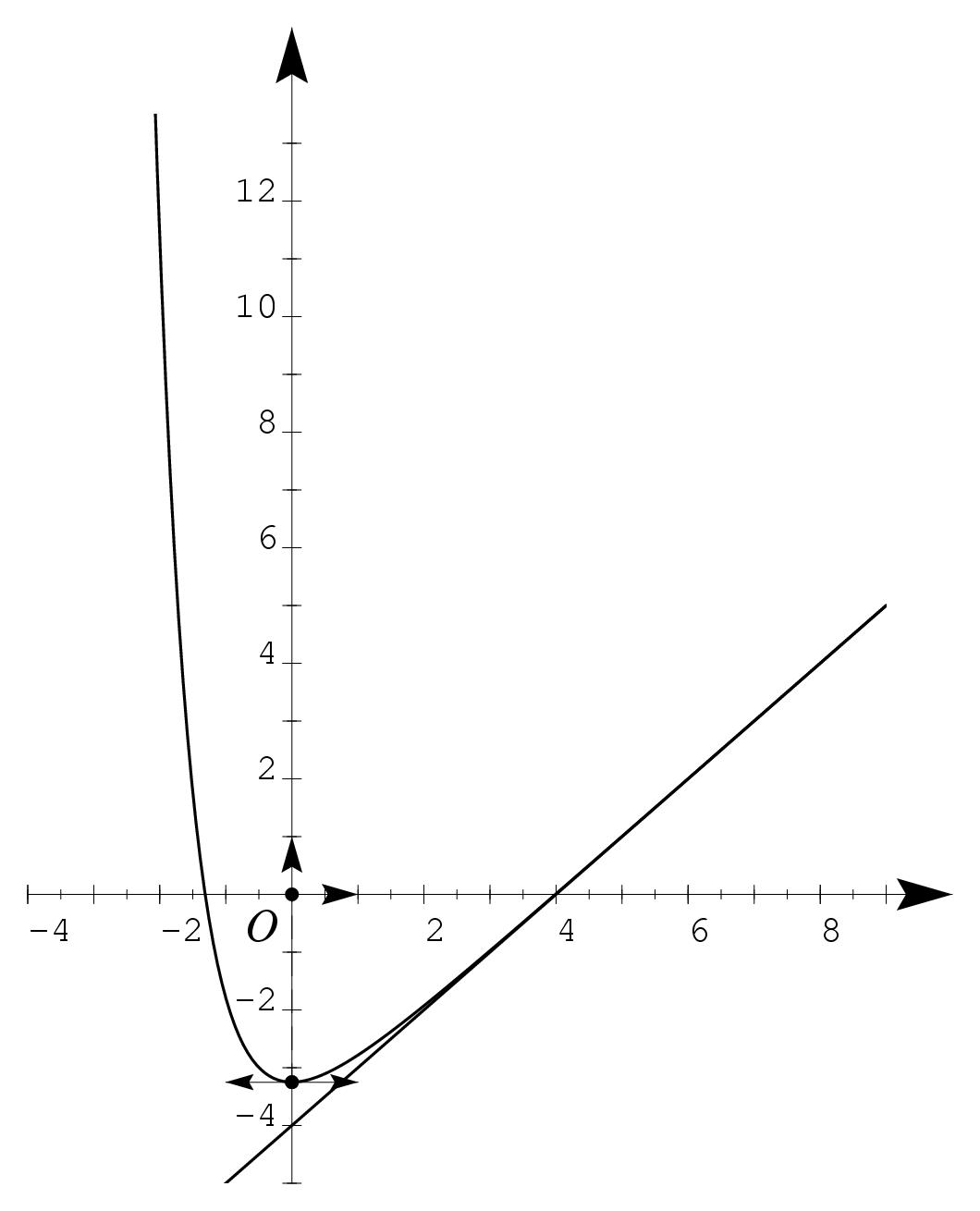
\exo{\'Equation différentielle du second ordre avec un polynôme} \let \partie \centerpartie \partie{A} On considère l'équation différentielle $$ y'' (x) + 3 y' (x) + 2 y (x) = 2x - 5 \leqno (E) $$ où $y$ est une fonction définie et deux fois dérivable de la variable $x$. \itemnum Résoudre l'équation différentielle $$ y'' (x) + 3 y' (x) + 2 y (x) = 0 \leqno (E_0) $$ \itemitemalphnum Déterminer les réels $a$ et $b$ tels que la fonction $x \mapsto ax + b$, notée $g$, soit une solution de $(E)$. \itemitemalph En déduire la solution générale de $(E)$. \itemnum Déterminer la fonction $f$ solution de $(E)$ qui vérifie les conditions initiales $$ f (0) = - {13 \over4} \qquad {\rm et } \qquad f' (0) = 0. $$ \partie{B} Soit $f$ la fonction définie sur l'ensemble $\rset$ des nombres réels par $$ f (x) = x - 4 + {1\over4} e^{-2x} + {1\over2} e^{-x}. $$ On note $C_f$ la courbe représentative de la fonction $f$ dans un repère orthonormal $(O, \vec \imath, \vec \jmath\/)$ d'unité graphique 2~cm. \itemitemalphnum Déterminer la limite de $f$ en $+\infty$. \itemitemalph En remarquant que $$ f (x) = e^{-x} \left( xe^x - 4 e^x + {1\over4} e^{-x} + {1\over2} \right) $$ déterminer la limite de $f$ en $-\infty$. \itemitemalphnum Calculer $f' (x)$ puis $f'' (x)$. \itemitemalph Montrer que, pour tout $x$ réel, $f'' (x) > 0$. En déduire le sens de variations de $f'$. \itemitemalph En remarquant que $f' (0) = 0$, déterminer le signe de $f' (x)$ suivant les valeurs du réel $x$. \itemitemalph Dresser le tableau de variation de la fonction $f$. \itemnum Calculer $\displaystyle{ \lim_{x \rightarrow +\infty} \big( f (x) - (x-4) \big) }$ et montrer que pour tout $x$ réel, l'expression $f (x) - (x-4)$ conserve un signe constant. \item{} Interpréter graphiquement les résultats de cette question. \itemnum Tracer la droite $D$ d'équation $y = x-4$ ainsi que la courbe $C_f$. \finexo \corrige{} \partie{A} \itemnum L'équation caractéristique de $(E_0)$ est $r^2 + 3r + 2 = 0$, et elle possède deux racines réelles $r_1 = -1$ et $r_2 = -2$. on en déduit que les solutions de $(E_0)$ sont toutes les fonctions $y$ ayant une écriture du type \mresultat{y = A e^{-x} + B e^{-2x}} où $A$ et $B$ désignent des constantes réelles quelconques. \itemalphnum Si $y = ax + b$, alors $y'= a$ et $y'' = 0$. On aura donc $y'' + 3y' + 2y = 2ax + (3a + 2b)$. Pour que $y$ soit une solution de $(E)$, il faut donc que soit vérifié le système $$ \cases{ 2 a = 2 \cr 3a + 2b = -5 \cr} \qquad \Longrightarrow \qquad \cases{ a = 1 \cr b = -4 \cr} \qquad \hbox{d'où la solution particulière} \qquad \mresultat{y = x-4}. $$ \itemalph La solution générale de $(E)$ est alors donnée par \mresultat{y = x-4 + A e^{-x} + B e^{-2x}} où $A$ et $B$ désignent des constantes réelles quelconques. \itemnum Si $f$ est une solution de $(E)$, alors elle possède une écriture comme celle donnée à la question précédente, et on a $f (0) = A + B - 4$, et $f' (0) = 1 - A - 2B$ En utilisant les conditions initiales, on trouve \mresultat{A = 1/2} et \mresultat{B = 1/4}, doù la solution cherchée~: $$ \dresultat{f (x) = x - 4 + {1\over4} e^{-2x} + {1\over2} e^{-x}} $$ \partie{B} \itemalphnum Comme $\lim_{+\infty} e^{-x} = \lim_{+\infty} e^{-2x} = 0$, on a facilement \dresultat{\lim_{x \rightarrow +\infty} f (x) = +\infty}. \itemalph Comme $\lim_{-\infty} xe^{x} = \lim_{-\infty} e^{x} = 0$ (cf formulaire), et que $\lim_{-\infty} e^{-x} = +\infty$, on a, par produit de limites et en utilisant la deuxième écriture de $f$, \dresultat{\lim_{x \rightarrow -\infty} f (x) = +\infty}. \itemalphnum On a \dresultat{f' (x) = 1 - {1\over2} e^{-2x} - {1\over2} e^{-x}} et \dresultat{f'' (x) = e^{-2x} + {1\over2} e^x}. \itemalph Comme l'exponentielle est toujours positive, on a $e^{-2x} > 0$ pour tout réel $x$, et $e^x > 0$ pour tout réel $x$. $f'' (x)$ étant la somme de deux nombres strictement positifs, on en déduit que \mresultat{\forall x \in \rset, f'' (x) > 0}, donc \tresultat{$f'$ est strictement croissante sur $\rset$}. \itemalph Vu la croissance stricte de $f'$, et comme $f' (0) = 0$, on en déduit que \tresultat{$f' (x) > 0$ pour $x>0$} et que \tresultat{$f' (x) < 0$ pour $x<0$}. \itemalph On obtient donc finalement le tableau de variation suivant pour $f$~: $$ \vcenter{\eightpoint\rm \def \hfq{\hfil \ } \offinterlineskip \halign{ % preamble &\hfq #\hfq \cr $x$& \vrule depth 5pt & $-\infty$&& $0$&& $+\infty$% \cr \noalign{\hrule} $f' (x)$& \vrule height 10pt depth 3pt && $-$& $0$& $+$ \cr \noalign{\hrule} \bbuucenter{$f (x)$}& \vrule& \bbuup{$+\infty$}& \bbrightddownarrow & \down{$-{13\over4}$}& \bbrightuuparrow & \bbuup{$+\infty$}& \cr }} $$ \itemnum On a $f (x) - (x-4) = {1\over4} e^{-2x} + {1\over2} e^{-x}$, donc \dresultat{\lim_{x \rightarrow +\infty} (f (x) - (x-4)) = 0} puisque $\lim_{+\infty} e^{-2x} = \lim_{+\infty} e^{-x} = 0$. De plus, $e^{-x}$ et $e^{-2x}$ étant deux nombres strictement positifs, leur somme sera un nombre strictement positif. D'où \mresultat{\forall x \in \rset, f (x) - (x-4) > 0}. Graphiquement, cela signifie que, si on note $D$ la droite d'équation $y = x-4$, alors \tresultat{$D$ est asymptote à $C_f$ en $+\infty$} et \tresultat{$C_f$ toujours au-dessus de $D$}. \def \epspath{% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} \epsfxsize = 80mm \itemnum $$ \superboxepsillustrate{equ2_009.ps} $$ \fincorrige