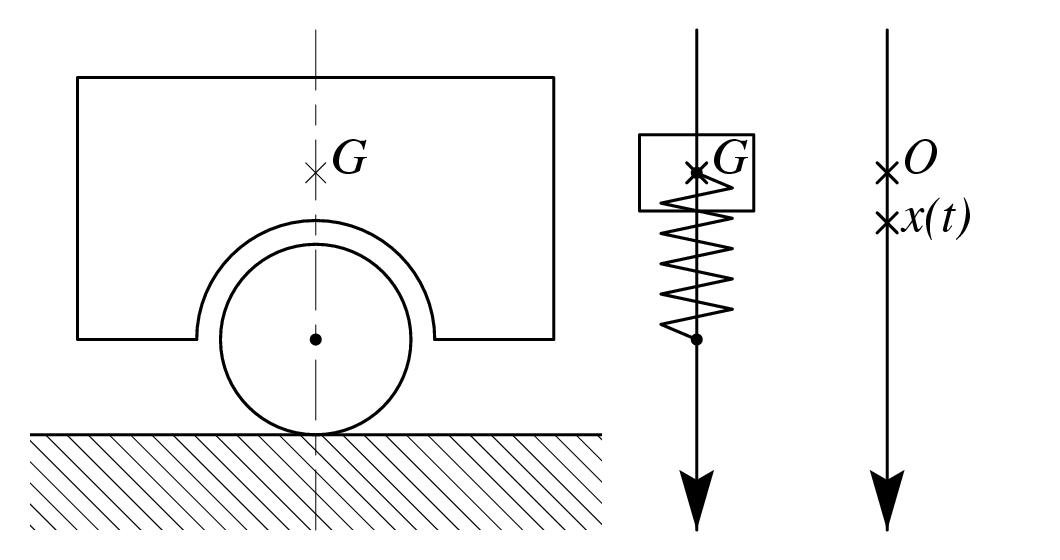
\exo{Suspension de remorque, {\rm bts mai}, {\sl 1996}} \let \partie \centerpartie L'objet de cet exercice est l'étude de la suspension d'une remorque dans les deux cas suivants~: système sans amortisseur puis avec amortisseurs. Le centre d'inertie $G$ d'une remorque se déplace sur un axe vertical$(O, \vec \imath\,)$ dirigé vers le bas (unité~: le mètre); il est repéré par son abscisse $x (t)$ en fonction du temps $t$ exprimé en secondes. On suppose que cette remorque à vide peut être assimilée à une masse $M$ ($M>0$) reposant sur un ressort fixé à l'axe des roues. \def \epspath{% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} \epsfxsize = 80mm $$ \epsillustrate{equ2_011.ps} $$ Le point $O$ est la position d'équilibre occupée par $G$ lorsque la remorque est vide. La remorque étant chargée d'une masse, on enlève cette masse et $G$ se met alors en mouvement. On considère que $t=0$ au premier passage de $G$ en $O$. \partie{A -- Mouvement non amorti} L'abscisse $x (t)$ de $G$ est alors, à tout instant $t$, solution de l'équation $M x'' (t) + k x (t) = 0$ où $k$ désigne la raideur du ressort, ce qui peut encore s'écrire~: $$ M x'' + kx = 0. \leqno (1) $$ On prend~: $M = 250\kg$ et $k = 6\, 250$~N.m$^{-1}$. Déterminer la solution particulière de l'équation différentielle $(1)$ vérifiant les conditions initiales $x (0) = 0$ et $x' (0) = -0, 10$~m.s$^{-1}$. Préciser la période de cette solution particulière. \partie{B -- Mouvement amorti} On équipe la remorque d'amortisseurs de constante d'amortissement $\lambda$. L'abscisse $x (t)$ du point $G$ vérifie alors à tout instant $t$ l'équation $Mx'' (t) + \lambda x' (t) + kx (t) = 0$, ce qui peut encore s'écrire $$ Mx'' + \lambda x' + kx = 0. \leqno (2) $$ On prend~: $M = 250\kg$, $k = 6\, 250$~N.m$^{-1}$ et $\lambda = 1\, 500$~N.s.m$^{-1}$. \itemitemalphnum Déterminer dans ces conditions la solution générale de l'équation différentielle $(2)$. \itemitemalph Sachant que $x (0) = 0$ et $x' (0) = - 0, 08$~m.s$^{-1}$, déterminer la solution particulière de l'équation $(2)$ définissant le mouvement de $G$. \itemnum On considère la fonction $f$ définie sur l'intervalle $[0, +\infty[$ par $f (t) = -0, 02 e^{-3t} \sin (4t)$. \itemitemalph Déterminer les valeurs de $t$ appartenant à l'intervalle $[0; 1,5]$ pour lesquelles $f (t) = 0$. \itemitemalph Déterminer la dérivée $f'$ de la fonction $f$. \itemitemalph On admet que, pour $a \neq 0$, les équations $$ a \sin \alpha + b \cos \alpha = 0 \qquad {\rm et} \qquad \tan \alpha = - {b \over a} \quad \hbox{(d'inconnue $\alpha$)} $$ ont les mêmes solutions. \itemitem{} Déterminer des valeurs approchée à $10^{-2}$ près des nombres réels $t$ appartenant à l'in\-ter\-val\-le $[0; 1, 5]$ et annulant $f' (t)$. Pour chaque valeur ainsi obtenue, préciser la valeur correspondante de $f (t)$. \itemitemalph Déduire des questions précédentes l'allure de la courbe $C_f$, représentative de $f$ dans le plan rapporté à un repère orthogonal. On prendra 10~cm (ou 10~grands carreaux) pour unité en abscisse, et 1~cm (ou 1~grand carreau) pour $0, 002$ unité en ordonnée. \finexo \corrige{} \let \partie \llappartie \partie{A} % Soit donc à résoudre l'équation différentielle $$ Mx'' + kx = 0. \leqno (1) $$ $\bullet$ L'équation caractéristique associée est~: \quad $Mr^2 + k = 0$, équation qui admet les deux racines complexes conjuguées $\pm i \sqrt{k/M} = \pm 5i$ avec les valeurs numériques de $M$ et $k$ données. On en déduit que les solutions de l'équation $(1)$ sont toutes les fonctions $x$ ayant une écriture du type $x = e^0 (A\cos (5t) + B \sin (5t))$ où $A, B$ constantes réelles quelconques, soit \dresultat{x (t) = A\cos (5t) + B \sin (5t) \quad \hbox{où $A, B$ constantes réelles quelconques}}. $\bullet$ Si $x$ est une solution de $(1)$, alors $x (0) = A$. De la condition initiale $x (0) = 0$, on en déduit que, pour la solution particulière cherchée, \mresultat{A=0}. $\bullet$ Toujours pour la solution particulière $x$ cherchée, on aura alors $x' (t) = 5B \cos (5t)$. La condition initiale $x' (0) = -0, 10$ donne alors \mresultat{B = -0, 02}. $\bullet$ Finalement, la solution de $(1)$ vérifiant les deux conditions initiales données est la fonction $x$ définie sur $\rset$ par \dresultat{x (t) = -0, 02 \sin {5t}}. % Cette fonction est périodique de période\dresultat{\omega = 2\pi /5}. \partie{B} % On considère maintenant l'équation $$ Mx'' + \lambda x' + kx = 0. \leqno (2) $$ \itemalphnum L'équation caractéristique associée est $$ Mr^2 + \lambda r + k = 0. $$ Son discriminant est $\Delta = \lambda^2 - 4Mk$, soit $\Delta = -4.10^6 = (2000 i)^2$ avec les valeurs numériques de $M$, $\lambda$ et $k$ données. L'équation caractéristique admet donc les deux racines complexes conjuguées $(-\lambda \pm 2000i) / 2M = -3 \pm 4i$. D'où la solution générale de l'équation $(2)$~: \dresultat{x (t) = e^{-3t} \big( A \cos (4t) + B \sin (4t) \big) } où $A$ et $B$ sont des constantes réelles quelconques. \itemalph De $x (0) = 0$, on en déduit que \mresultat{A = 0} puisque $x (0) = A$. \item{} On a alors $x' (t) = -3 e^{-3t} \times B \sin (4t) + 4B e^{-3t} \cos (4t)$, et donc $x' (0) = 4B$. De la condition initiale $x' (0) = -0, 08$, on tire alors \mresultat{B = -0, 02}. La solution particulière cherchée est donc la fonction $x$ définie sur $\rset$ par \dresultat{x (t) = -0, 02e ^{-3t} \sin (4t)}. \itemalphnum Sans surprise, la fonction $f$ à étudier est la solution particulière que l'on vient de trouver à la question précédente. Comme $e^{-3t}$ est toujours non nul, on a $$ f (t) = 0 \qquad \Longleftrightarrow \qquad \sin (4t) = 0 \qquad \Longleftrightarrow \qquad 4t = k \pi, \quad k \in \zset \qquad \Longleftrightarrow \qquad \dresultat{t = k {\pi \over4}, \quad k \in \zset} $$ Sur l'intervalle $[0; 1, 5]$, l'équation $f (t) = 0$ admet donc les deux solutions~: \dresultat{0 \ {\rm et}\ {\pi \over4}}. \itemalph On trouve $f' (t) = 0, 06 e^{-3t} \sin (4t) - 0, 08 e^{-3t} \cos (4t)$, soit \dresultat{f' (t) = 0, 02 e^{-3t} \big( 3 \sin (4t) - 4 \cos (4t) \big) }. \itemalph Comme $0, 02 e^{-3t}$ est toujours différent de $0$, il vient~: $$\displaylines{ f' (t) = 0 \qquad \Longleftrightarrow \qquad 3 \sin (4t) - 4 \cos (4t) = 0 \qquad \Longleftrightarrow \qquad \tan (4x) = {4\over3} \cr \Longleftrightarrow \qquad 4x = \arctan \left( {4\over3} \right) + k\pi, \quad k \in \zset \qquad \Longleftrightarrow \qquad x = {1\over4} \arctan \left( {4\over3} \right) + k {\pi \over4}, \quad k \in \zset \cr }$$ En essayant différentes valeurs de $k$, on trouve que l'équation $f' (t) = 0$ admet deux solutions $t_1$ et $t_2$ (pour $k=0$ et $k=1$) dans l'intervalle $[0; 1, 5]$. On a \mresultat{t_1 \approx 0, 23} et \mresultat{t_2 \approx 1, 02}. Les valeurs correspondantes de $f$ sont \mresultat{f (t_1) \approx 0, 008} et \mresultat{f (t_2) \approx 0, 000\, 8}. \def \epspath{% $HOME/tex_doc/lycee/database//btsmai/analyse/equadiff/} \epsfxsize = 150mm \itemalph $$ \superboxepsillustrate{equ2_011b.ps} $$ \fincorrige