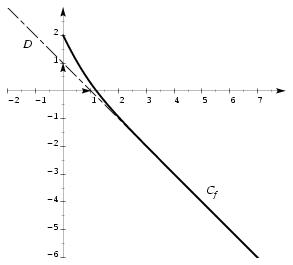
\exo {Une solution particulière est affine} \let \partie \centerpartie Le plan est rapporté à un repère orthonormal $(O, \vec \imath , \vec \jmath )$. \partie {A} On considère l'équation différentielle $$ y'' + 4y' + 4y = -4x \leqno (E) $$ où $y$ désigne une fonction inconnue de la variable réelle $x$, définie et deux fois dérivable sur $\rset $. \itemnum Donner la solution générale de l'équation sans second membre associée à $(E)$. \itemnum Vérifier que la fonction qui à tout réel $x$ associe $-x+1$ est une solution particulière de $(E)$. \itemnum Déduire des deux questions précédentes la solution générale de $(E)$. \itemnum Déterminer la solution $\varphi $ de $(E)$ dont la courbe représentative passe par le point $A$ de coordonnées $(0, 2)$ et admet en ce point une tangente de coefficient directeur $-2$. \partie {B} Soit $f$ la fonction définie sur $[0, +\infty [$ par $$ f (x) = -x + 1 + (x+1) e^{-2x} $$ et soit $C_f$ sa courbe représentative dans le repère $(O, \vec \imath , \vec \jmath )$ (unité graphique~: 4~cm ou 4~grand carreaux). \itemitemalphnum Calculer la limite de $f (x)$ lorsque $x$ tend vers $+\infty $. \itemitemalph On pose $$ g (x) = f (x) - (-x+1). $$ Déterminer le signe de $g (x)$ et déterminer la limite de $g (x)$ lorsque $x$ tend vers $+\infty $. \itemitem {} Interpréter graphiquement les résultats obtenus. \itemitemalphnum Montrer que la dérivée $f'$ de $f$ vérifie $$ f' (x) = - (2x+1) e^{-2x} - 1. $$ \itemitemalph En déduire le sens de variation de $f$ sur $[0, +\infty [$, puis construire le tableau de variation de $f$ sur cet intervalle. \itemnum Construire la droite $D$ d'équation $y = -x+1$ et la courbe $C_f$. \finexo \corrige {} \let \partie \llappartie \partie {A} \vskip -5\parskip \itemnum L'équation caractéristique associée à l'équation sans second membre $(E_0)$ est $$ r^2 - 4y + 4 = 0. $$ Son discriminant $\Delta $ est nul, et sa seule racine est $r = -2$, d'où la solution générale de $(E_0)$~: \dresultat {y = (Ax+B) e^{-2x}} où $A$ et $B$ sont des constantes réelles quelconques. \itemnum Si $g (x) = -x+1$, alors $g' (x) = -1$ et $g'' (x) = 0$. On vérifie alors facilement que $g''+4g'+4g = -4x$, autrement dit que \tresultat {$g=-x+1$ est une solution particulière de $(E)$}. \itemnum En conclusion, la solution générale de $(E)$ est l'ensemble des fonctions $y$ ayant une écriture du type $$ \dresultat {y (x) = -x+1 + (Ax+B) e^{-2x}} \qquad {\rm où} \qquad \hbox {$A$ et $B$ constantes réelles quelconques.} $$ \itemnum Soit $\varphi $ l'une de ces solutions. Les conditions initiales imposent $\varphi (0) = 2$ (la courbe passe par $A (0, 2)$) et $\varphi ' (0) = 0$ (tangente horizontale en $A$). Comme on a $\varphi ' (x) = -1 + (-2Ax +A-2BH) e^{-2x}$, il vient les 2~équations~: $$ 1+B = 2 \qquad {\rm et} \qquad -1+A-2 = -2 $$ d'où l'on tire $(A, B) = (1, 1)$. Fionalement, la so:ution cherchée est la fonction $\varphi $ définie sur $\rset $ par $$ \dresultat {\varphi (x) = -x + 1 + (x+1) e^{-2x}} $$ \partie {B} \vskip -5\parskip \itemnum On a \dresultat {\lim _{x\to +\infty } f (x) = -\infty } puisque $$ f (x) = -x + 1 + (x+1) e^{-2x} \qquad {\rm avec} \qquad \cases { \lim _{x\to +\infty } -x+1 = -\infty \cr \lim _{x\to +\infty } (x+1) e^{-2x} = 0 \cr } $$ La deuxième limite provenant du fait que lorsque $x$ tend vers $+\infty $, la fonction exponentielle va plus vite que toute fonction polynôme. \itemalphnum On a donc $g (x) = (x+1) e^{-2x}$. D'où \dresultat {\lim _{x\to +\infty } g (x) = 0} en vertu des calculs de la question précédente. De plus $g (x)$ est du signe de $(x+1)$ puisque $e^{-2x}$ est toujours positif. Comme $x\in [0, +\infty [$, on en déduit que \tresultat {$g$ est toujours positif}. \item {} Géométriquement, en notant $D$ la droite d'équation $y = -x+1$, ces résultats signifient que $$ \tresultat {$D$ est asymptote à la courbe $C_f$ en $+\infty $} \quad \hbox { et } \quad \tresultat {la courbe $C_f$ est toujours au-dessus de $D$}. $$ \itemalphnum On trouve $f' (x) = -1 + e^{-2x} (1-2x62)$, d'où \dresultat {f' (x) = - (2x+1) e^{-2x} - 1}. \itemalph Les nombres $e^{-2x}$ et $(2x+1)$ sont toujours positifs sur $[0, +\infty [$, donc $-(2x+1) e^{-2dx}$ est toujours négatif sur l'intervalle considéré, et \tresultat {$f' (x)$ est toujours négatif} puisque somme de 2~nombres négatifs. D'où le tableau de variation de $f$~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& 2&& +\infty \cr \noalign {\hrule height 1pt } f' (x)&& &- \cr \noalign {\hrule height 1pt} \bucenter {$f (x)$}&& \bup {$2$}& \brightdownarrow & \down {$-\infty $} \cr }} }$$ \def \epspath {% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} \itemnum Et sa courbe représentative~: $$ \superboxepsillustrate {equ2_018.ps} $$ \fincorrige