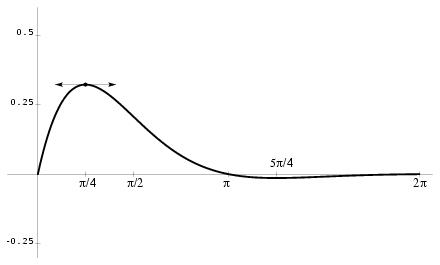
\exo {\' Equation différentielle linéaire du second ordre} En électronique, l'étude d'un circuit conduit à l'équation différentielle $$ x'' + 2x' + 2x = 0 \leqno (E) $$ dans laquelle $x$ désigne une fonction numérique de la variable $t$, admettant des dérivées première et seconde notées respectivement $x'$ et $x''$. \itemnum Résoudre cette équation sur $\rset $. \itemnum Déterminer la solution particulière de cette équation prenant la valeur 0 pour $t=0$ et dont la dérivée prend la valeur $1$ pour $t=0$. \itemnum Soit $f$ la fonction numérique telle que, pour tout élément $t$ de l'intervalle $[0, 2\pi]$, $$ f (t) = e^{-t} \sin t. $$ \itemitemalph Vérifier que, pour tout $t$ réel, on a $$ \cos t - \sin t = \sqrt 2 \cos \left( t + {\pi \over 4}\right) . $$ \itemitemalph \' Etudier les variations de $f$ sur $[0, 2\pi ]$ et dresser son tableau de variation. \itemitemalph Tracer $C_f$, la courbe représentative de la fonction $f$ dans le plan rapporté à un repère orthogonal où l'unité vaut 2~cm sur l'axe des abscisses et 10~cm sur l'axe des ordonnées. \itemnum On se propose de calculer, en $\cm ^2$, une valeur approchée par défaut à $1\mm ^2$ près de l'aire du domaine plan délimité par la courbe $C_f$, l'axe des abscisses, l'axe des ordonnées et la droite verticale $x=\pi $. \item {} \` A cette fin, deux méthodes sont proposées~: \itemitemalph Calculer l'intégrale $$ \int _0^\pi f (t) \, dt $$ au moyen de deux intégrations par parties successives. \itemitemalph En utilisant l'équation différentielle $(E)$ écrite sous la forme $$ x = - {1\over 2} (x'' + 2x'), $$ déterminer une primitive $F$ de $f$ sur $[O, \pi]$. \itemitem {} En déduire l'expression de $\displaystyle \int _0^\pi f (t)\, dt$ à l'aide de $F$. \itemitemalph Déterminer une valeur approchée de l'aire considérée à $1\mm ^2$ près par défaut. \finexo \corrige {} \itemnum L'équation caractéristique associée à $(E)$ est $r^2 + 2r + 2 = 0$, de discriminant $\Delta = -4 = (2i)^2$, et de racines $r = -1\pm i$. On en déduit la solution générale de $(E)$~: \dresultat {y (t) = e^{-t} (A\cos t + B \sin t)} où $A$ et $B$ sont des constantes réelles arbitraires. \itemnum La condition initiale $y (0) = 0$ entraîne immédiatement que $A = 0$. Et comme $$ y' (t) = -e^{-t} \big( (B-A)\cos t - (B+A) \sin t\big) $$ la condition $y' (0) = 1$ entraîne que $B = 1$. La solution particulière de $(E)$ vérifiant les conditions initiales est donc la fonction $f$ définie par \dresultat {f (t) = e^{-t}\sin t}. \itemalphnum En développant le cosinus avec la formule $\cos (a+b) = \cos \cos b - \sin a\sin b$, on obtient immédiatement la relation demandée. \itemalph $\bullet $ On trouve $$ \dresultat {f' (t) = e^{-t} (\cos t - \sin t) = \sqrt 2 e^{-t} \cos \left( t + {\pi \over 4}\right)} $$ Cette dérivée est évidemment du signe de $\cos ( t + {\pi \over 4})$ puisque l'exponentielle est toujours positive. \item {} $\bullet $ Cherchons les zéros de la dérivée. On a $$ f' (t) = 0 \quad \Longleftrightarrow \quad \cos \left( t + {\pi \over 4}\right) = 0 \quad \Longleftrightarrow \quad t + {\pi \over 4} = {\pi \over 2} \pmod \pi \quad \Longleftrightarrow \quad \dresultat {t = {\pi \over 4} \pmod \pi} $$ Sur l'intervalle $[0, 2\pi]$, la dérivée $f'$ s'annule donc 2~fois~: en $\pi /4$ et en $5\pi /4$. On vérifie alors facilement que $f' (0)$ et $f' (2\pi)$ sont positifs, alors que $f' (\pi /2)$ est négatif. \item {} $\bullet $ D'où le tableau de variation de $f$ sur $[0, 2\pi ]$~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr t&& 0&& \pi /4&& 5\pi /4&& 2\pi & \cr \noalign {\hrule height 1pt} f' (t)&& &+& 0&-& 0&+& & \cr \noalign {\hrule height 1pt} \buucenter {$f (t)$}&& \down {0}& \brightuuparrow & \buup {${\sqrt 2\over 2}e^{-\pi /4}$}& \brightddownarrow & \down{$-{\sqrt 2\over 2}e^{-5\pi /4}$}& \brightuuparrow & \buup {0} \cr }} }$$ \def \epspath {% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} \itemalph $$ \superboxepsillustrate {equ2_021.ps} $$ \itemalphnum $$\eqalign { K &= \int _0^\pi e^{-t} \sin t \, dt. \qquad \hbox {de la forme} \qquad \int U' V \quad {\rm avec} \quad \cases { U' = e^{-t} &\quad $U = -e^{-t}$ \cr V = \sin t &\quad $V' = \cos t$ \cr } \cr &= \underbrace {\Big[ - e^{-t}\sin t\Big] _0^\pi}_{0} + \int _0^\pi e^{-t}\cos t \, dt \cr &= \int _0^\pi e^{-t} \cos t \, dt \qquad \hbox {de la forme} \qquad \int U' V \quad {\rm avec} \quad \cases { U' = e^{-t} &\quad $U = -e^{-t}$ \cr V = \cos t &\quad $V' = -\sin t$ \cr } \cr &= \Big[ - e^{-t}\cos t\Big] _0^\pi - \underbrace {\int _0^\pi e^{-t}\sin t \, dt}_{K} = e^{-\pi} + 1 - K \cr }$$ On en déduit que $2K = 1 + e^{-\pi }$, et donc que \dresultat {K = {1\over 2} (1+e^{-\pi })}. \itemalph Sachant que la fonction $f$ est solution de $(E)$, on en déduit qu'elle vérifie la relation $$ f = - {1\over 2} (f'' + 2f'). $$ Une primitive $F$ de $f$ vérifiera alors la relation $$ F = - {1\over 2} (f' + 2f). $$ On en conclut que la fonction $F$ définie par $$ F (t) = - {1\over 2} e^{-t} (\cos t - \sin t + 2\sin t), \qquad {\rm soit} \qquad \dresultat {F (t) = - {1\over 2} e^{-t} (\cos t +\sin t)} $$ est une primitive de la fonction $f$. \item {} Il vient alors $K = F (\pi ) - F (0)$, soit \dresultat {K = {1\over 2} (1+e^{-\pi })}. \itemalph L'unité d'aire étant de $10\cm \times 2\cm = 20\cm ^2$, on trouve que l'aire cherchée fait environ $10, 43\cm ^2$, soit environ \dresultat {1\, 043\mm ^2} à $1\mm ^2$~ près par défaut. \fincorrige