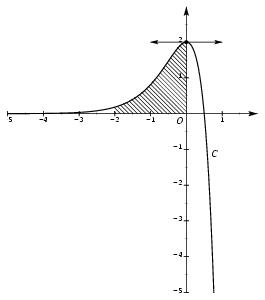
\exo {\' Equation différentielle d'ordre 2, {\sl bts mai, session 1997}} \let \partie \centerpartie \partie {A - Résolution d'une équation différentielle} On considère l'équation différentielle $(E)$ définie sur $\rset $ par : $$ y '' - 3 y ' + 2 y = - 4 e^{2 x}. \leqno (E) $$ \itemnum Donner la forme générale des solutions de l'équation $(E ' )$~: $$ y '' - 3 y ' + 2 y = 0. \leqno (E') $$ \itemnum Déterminer le réel a pour que la fonction g définie sur $\rset $ par $g (x) = a x e^{2x}$ soit solution de l'équation $(E)$. \itemitemalphnum Déduire des questions précédentes la solution générale de l'équation $(E)$. \itemitemalph Déterminer la solution $f$ de l'équation $(E)$ dont la courbe représentative passe par le point $S(0 ; 2)$ et admet en ce point une tangente parallèle à l'axe des abscisses. \partie {B - \'Etude d'une solution particulière de l'équation différentielle $(E)$} Soit $f$ la fonction définie sur $\rset $ par : $$ f(x) = 2 e^{2 x} (1 - 2 x). $$ On appelle $C$ la courbe représentative de $f$ dans un repère orthonormal ; unité graphique~: $2\cm $. \itemitemalphnum \' Etudier la limite de $f$ en $+\infty $ \itemitemalph \' Etudier la limite de $f$ en $-\infty $ . \itemitem {} En déduire que $C$ admet une asymptote (que l'on précisera). Préciser la position de $C$ par rapport à cette asymptote. \itemnum \' Etudier les variations de la fonction $f$ sur $\rset $. \itemnum Tracer la courbe $C$. \itemnum \` A l'aide d'une intégration par parties, déterminer l'aire, exprimée en $\cm ^2$, du domaine limité par $C$, l'axe des abscisses et les droites d'équations $x = - 2$ et $x = 0$. Donner la valeur de cette aire arrondie au $\mm ^2$. \finexo \corrige \let \partie \llappartie \partie {A} % \vskip -5mm \itemnum L'équation caractéristique est $r^2 - 3r + 2 = 0$. Son discriminant est $\Delta = 1$, d'où les $2$~racines $r_1 = 2$ et $r_2 = 1$. La solution générale de $(E')$ est donc \dresultat {y_0 (x) = Ae^x + Be^{2x}}, où $A$ et $B$ sont des constantes réelles quelconques. \itemnum On trouve $$ g (x) = ax e^{2x}, \qquad \qquad g' (x) = (2ax + a) e^{2x}, \qquad \qquad g'' (x) = (4ax + 4a) e^{2x}. $$ D'où $$\eqalign { g'' - 3g' + 2 g &= \big( (4ax + 4a) - 3(2ax + a) + 2ax \big) e^{2x} \cr &= a e^{2x} \cr }$$ Pour avoir $g$ solution de $(E)$, il faut avoir $a = -4$, d'où la solution particulière de $(E)$~: \dresultat {g (x) = -4xe^{2x}}. \itemalphnum La solution générale de $(E)$ est donc \dresultat {y (x) = -4xe^{2x} + Ae^x + Be^{2x}}, où $A$ et $B$ sont des constantes réelles quelconques. \itemalph La fonction $f$ est solution de $(E)$, et vérifie \dresultat {f (0) = 2} et \dresultat {f' (0) = 2}. Comme on a $y' (x) = -4e^{2x} -8xe^{2x} + Ae^x + 2Be^{2x}$, on en déduit le système $$\displaylines { \cases { f (0) = 2 \cr f' (0) = 0 \cr} \quad \Longrightarrow \quad \matrix { \eightpoint \rm (1)\cr \eightpoint \rm (2)\cr} \cases { A + B = 2 \cr -4 + A + 2B = 0 \cr} \quad \Longrightarrow \quad \matrix { \cr \eightpoint \rm (2) - (1)\cr} \cases { A + B = 2 \cr -4 + B = -2 \cr} \cr \quad \Longrightarrow \quad (A, B) = (0, 2) }$$ d'où la solution cherchée~: \dresultat {f (x) = -4xe^{2x} + 2e^{2x}}, soit encore \dresultat {f (x) = 2e^{2x} (1-2x)}. \partie {B} % \vskip -5mm \itemalphnum On a \dresultat { \lim _{x\to +\infty } f (x) = -\infty } car $f (x) = 2e^{2x} (1-2x)$ avec $\lim _{+\infty } 2e^{2x} = +\infty $ et $\lim _{+\infty } (1-2x) = -\infty $. \itemalph On a \dresultat { \lim _{x\to -\infty } f (x) = 0 } car $f (x) = 2e^{2x} (1-2x)$ avec $\lim _{-\infty } 2e^{2x} = 0$ (en l'$\infty $, l'exponentielle l'emporte sur le polynôme). \item {} On en déduit que l'axe $Ox$, d'équation \tresultat {$y=0$ est asymptote horizontale} à la courbe de $f$. Une étude du signe de $f (x)$ nous donne la position par rapport à $Ox$~: $$\dresultat { \vcenter{\offinterlineskip \halign{ % preamble & \cc {$#$}& #& $#$ & \cc {$#$}& \cc {$#$}& \cc {$#$}& \cc {$#$}& $#$ \cr x& \tv & \, -\infty && 1/2 && +\infty \cr \noalign{\hrule} 2e^{2x} & \tv && + &\tv & + & \cr \noalign{\hrule} 1-2x & \tv && + & 0 & - & \cr \noalign{\hrule} f (x) & \tv && + & 0 & - & \cr \noalign{\hrule} \tvi height 15pt depth 10pt \hbox {positions relatives}& \tv && \matrix{C_f {\rm \ au}\cr {\rm dessus\ de\ } Ox }& \tv & \matrix{C_f {\rm \ au}\cr {\rm dessous\ de\ } Ox } \cr }} }$$ \itemnum Il vient $f' (x) = 4e^{2x}(1-2x) - 4e^{2x}$, soit \dresultat {f' (x) = -8xe^{2x}} du signe de $-8x$ car $e^{2x}$ est toujours positif. D'où le tableau~: $$\vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -\infty && 0&& +\infty \cr \noalign {\hrule height 1pt } f' (x)&& &+& 0& - \cr \noalign {\hrule height 1pt} \buucenter {$f (x)$}&& \down {$0$}& \brightuuparrow & \buup {$2$}& \brightddownarrow & \down{$-\infty $} \cr }} $$ \def \epspath{% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} \itemnum Et la courbe~: $$ \superboxepsillustrate {equ2_029.ps} $$ \itemnum L'unité d'aire étant de $2\cm \times 2\cm = 4\cm ^2$, nous avons donc $$\displaylines { {\cal A} = 4\times \int _{-2}^0 f (x) \,dx = 4\times \int _{-2}^0 2e^{2x} (1-2x) \,dx \cr \hbox {du type} \quad \int U'V \quad {\rm avec} \quad \cases { U' = 2e^{2x} \cr V = 1-2x \cr} \quad \Longrightarrow \quad \cases { U = e^{2x} \cr V' = -2 \cr} }$$ Le calcul de l'intégrale donne alors $$\eqalign { \int _{-2}^0 2e^{2x} (1-2x) \,dx &= \Big[ e^{2x} (1-2x)\Big]_{-2}^0 - \int _{-2}^0 -2e^{2x} \,dx \cr &= 1 - 5e^{-4} + \Big[ e^{2x}\Big] _{-2}^0 = 1 - 5e^{-4} + 1 - e^{-4} \cr &= 2 - 6e^{-4} \qquad {\rm d'où}\qquad \dresultat {{\cal A} = 8 - 12e^{-4} \cm ^2\approx 778\mm ^2}. \cr }$$ \fincorrige