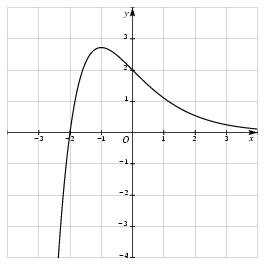
\exo {\' Equation différentielle, étude de fonction, {\sl bts mai, session 2006}} \centerline {\bf Les trois parties de cet exercice peuvent être traitées de façon indépendante.} \let \partie \centerpartie \partie {A - Résolution d'une équation différentielle} On considère l'équation différentielle $$ y'' - 3y' - 4y = -5e^{-x} \leqno (E) $$ où $y$ est une fonction de la variable $x$, définie et deux fois dérivable sur $\rset $, $y'$ la fonction dérivée de $y$, et $y''$ sa fonction dérivée seconde. \itemnum Déterminer les solutions sur $\rset $ de l'équation différentielle~: $$ y'' - 3y' - 4y = 0 \leqno (E_0) $$ \itemnum Soit $h$ la fonction définie sur $\rset $ par~: \qquad $h (x) = xe^{-x}$. \item {} Démontrer que la fonction $h$ est une solution particulière de l'équation différentielle $(E)$. \itemnum En déduire l'ensemble des solutions de l'équation différentielle $(E)$. \itemnum Déterminer la solution $f$ de l'équation $(E)$ qui vérifie les conditions initiales $f (0) = 2$ et $f' (0) = -1$. \partie {B - \' Etude locale d'une fonction} La courbe $C$ ci-dessous est la représentation graphique, dans un repère orthonormal $(O; \vec \imath , \vec \jmath \/)$, de la fonction $f$ définie sur $\rset $ par $f (x) = (x + 2) e^{-x}$. \def \epspath { $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} $$ \superboxepsillustrate {equ2_033.ps} $$ \itemnum Démontrer que le développement limité à l'ordre $3$, au voisinage de $0$, de la fonction $f$ est $$ f (x) = 2 - x + {x^3\over 6} + x^3 \varepsilon (x) \qquad {\rm avec} \qquad \lim _{x \to 0} \varepsilon (x) = 0. $$ \itemnum Déduire du {\bf 1.} une équation de la tangente $T$ à la courbe $C$ au point d'abscisse $0$. \itemnum \' Etudier la position relative de $C$ et $T$ au voisinage du point d'abscisse $0$. \partie {C - Calcul intégral} On note $\displaystyle { I = \int _0^{0,6} f (x) \, dx }$. \itemnum \` A l'aide d'une intégration par parties, démontrer que $I = 3 - 3, 6 e^{-0, 6}$. \itemnum Donner la valeur approchée arrondie à $10^{-3}$ de $I$. \itemnum Donner une interprétation graphique du nombre $I$. \finexo \corrige \let \partie \llappartie \partie {A} \vskip -5mm % \itemnum L'équation caractéristique associée à $(E_0)$ est~: $r^2 - 3r - 4 = 0$, de discriminant $\Delta = 25$, d'où les $2$~racines $x_1 = 4$ et $x_2 = -1$. D'où la \tresultat {solution générale de $(E_0)$~: $y_0 = A e^{4x} + Be^{-x}, A, B \in \rset $}. \itemnum On a $$ h (x) = xe^{-x}, \qquad \qquad h' (x) = (1-x) e^{-x}, \qquad {\rm et}\qquad h'' (x) = (x-2) e^{-x} $$ d'où $$\eqalign { h'' - 3h' - 4h &= \big( (x-2) -3 (1-x) - 4x\big) e^{-x} \cr &= -5e^{-x} }$$ ce qui prouve que \tresultat {$h (x) = xe^{-x}$ est solution particulière de $(E)$}. \itemnum Donc \tresultat {la solution générale de $(E)$ est $y (x) = xe^{-x} + A e^{4x} + Be^{-x}, A, B \in \rset $} \itemnum En partant du résultat ci-dessus, on obtient $$ y' (x) = (1-x) e^{-x} + 4Ae^{4x} - Be^{-x}. $$ Les conditions initiales nous imposent alors le système $$ \cases { f (0) = 2 \cr f' (0) = -1 \cr } \Leftrightarrow \cases { A + B = 2 \cr 1 + 4A - B = -1 \cr } \Leftrightarrow \matrix { \eightpoint \rm (1) \cr \eightpoint \rm (2) \cr } \cases { A + B = 2 \cr 4A - B = -2 \cr } \Leftrightarrow \matrix { \eightpoint \rm (1) + (2) \cr \cr } \cases { 5A = 0 \cr 4A - B = -2 \cr } $$ d'où l'on tire $(A, B) = (0, 2)$, d'où la \tresultat {solution particulière cherchée~: $f (x) = (x+2) e^{-x}$}. \partie {B} \vskip -5mm % \itemnum En utilisant le formulaire, il vient $$ e^{-x} = 1 - x + {x^2\over 2} - {x^3\over 6} + x^3\varepsilon (x) \qquad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0. $$ Multiplions maintenant cette égalité par $(x+2)$, on obtient $$\eqalign { (x-2) e^{-x} &= (x+2) \left( 1 - x + {x^2\over 2} - {x^3\over 6} \right) + x^3\varepsilon (x) \qquad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0 \cr &= x - x^2 + {x^3\over 2} + 2 - 2x + x^2 - {x^3\over 3} + x^3\varepsilon (x) \qquad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0 \cr &= \dresultat {f (x) = 2 - x + {x^3\over 6} + x^3\varepsilon (x) \qquad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0} \cr }$$ \itemnum L'équation de la tangente cherchée est le développement limité d'ordre 1 en $0$ de $f (x)$. D'où l'équation cherchée~: \dresultat {T~: y = 2-x}. \itemnum \' Etudier la position relative de $C$ et $T$ revient à étudier le signe de la différence $f (x) - T (x)$. Comme l'étude se fait au voisinage de $0$, on peut utiliser le développement limité précédent. D'où $$ f (x) - T (x) = {x^3\over 6} + x^3\varepsilon (x) \qquad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0 $$ Cette différence est du signe de $x^3$, et on conclue aisément~: $$\dresultat { \vcenter{\offinterlineskip \halign{ % preamble & \cc {$#$}& #& $#$ & \cc {$#$}& \cc {$#$}& \cc {$#$}& \cc {$#$}& $#$ \cr x& \tv & \, && 0 && \cr \noalign{\hrule} f (x) - T (x)& \tv && - & 0 & + & \cr \noalign{\hrule} \tvi height 15pt depth 10pt \hbox {positions relatives}& \tv && \matrix{C_f {\rm \ au}\cr {\rm dessous\ de\ } T }& \tv & \matrix{C_f {\rm \ au}\cr {\rm dessus\ de\ } T } \cr }} }$$ \partie {C} \vskip -5mm % \itemnum \` A calculer l'intégrale $$ I = \int _0^{0, 6} \underbrace {(x+2)}_{U} \underbrace {e^{-x}}_{V'} \, dx \qquad {\rm avec} \qquad \cases { U' = 1 \cr V = -e^{-x} \cr } $$ Il vient alors $$\eqalign { I &= \Big[ - (x+2) e^{-x}\Big] _0^{0, 6} - \int _0^{0, 6} -e^{-x}\, dx \cr &= \Big( -2, 6 e^{-0, 6} +2 \Big) - \Big[ e^{-x}\Big] _0^{0, 6} \cr &= \Big( -2, 6e^{-0, 6} +2 \Big) - \Big( e^{-0, 6} - 1\Big) \qquad {\rm soit} \qquad \dresultat {I = 3 - 3,6e^{-0, 6}}. \cr }$$ \itemnum Il vient \dresultat {I \approx 1, 024} \itemnum Ce nombre représente l'aire, en unité d'aire, du domaine plan limité par la courbe de $f$, l'axe $Ox$, l'axe $Oy$ et la droite verticale $x = 0, 6$ (aire hachurée sur le dessin ci-dessous). \def \epspath { $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} $$ \superboxepsillustrate {equ2_033a.ps} $$ \fincorrige