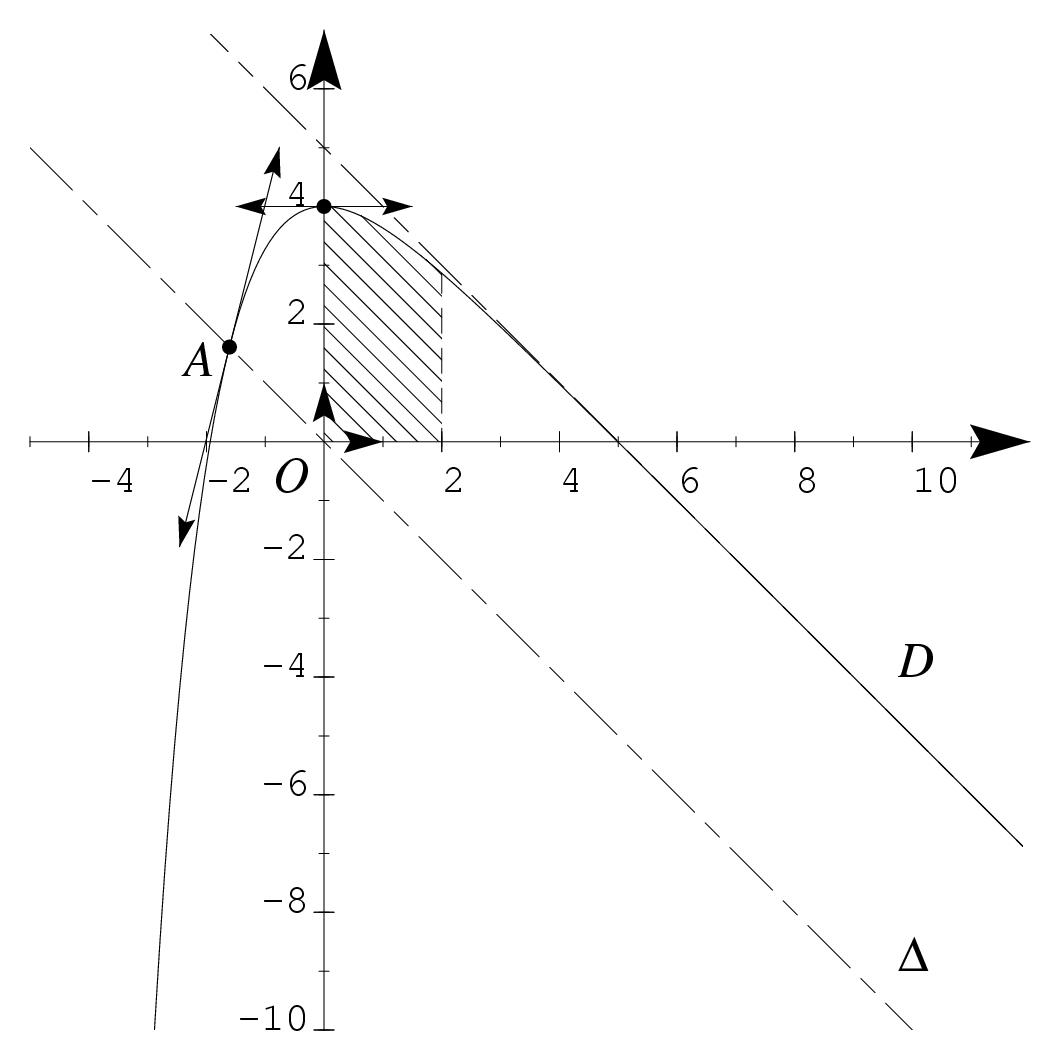
\exo{\'Etude d'une fonction exponentielle, {\rm bac F1}, {\sl 1994}} Soit $f$ la fonction numérique définie sur l'ensemble des nombres réels $\rset$ par $$ f (x) = 5 - x - e^{-x}. $$ On désigne par $\cal C$ sa courbe représentative dans un repère orthonormal d'unité graphique 1~cm. \itemitemalphnum Déterminer la limite de $f$ en $+\infty $. \itemitemalph Démontrer que $f (x)$ tend vers $-\infty$ lorsque $x$ tend vers $-\infty$. \itemnum \'Etudier les variations de la fonction $f$ et donner le tableau de variation. \itemitemalphnum Montrer que la droite $D$ d'équation $y = -x + 5$ est asymptote à la courbe $\cal C$. \itemitemalph \'Etudier la position relative de $\cal C$ et $D$. \itemnum On considère la droite $\Delta$ d'équation $y = -x$. \itemitemalph Calculer les coordonnées de $A$, le point d'intersection de $\Delta$ et $\cal C$. \itemitemalph Calculer le coefficient directeur de la tangente en $A$ à $\cal C$ et tracer cette tangente. \itemnum Construire $\cal C$ et $D$ avec précision. \itemnum Calculer, en cm$^2$, l'aire du domaine plan limité par $\cal C$, l'axe des abscisses, l'axe des ordonnées et la droite d'équation $x=2$. On donnera la valeur exacte de cette aire puis la valeur approchée, arrondie au mm$^2$. \finexo \corrige{} \everymath = {\displaystyle } \itemalphnum On a \dresultat{\lim_{x \to +\infty} f (x) = -\infty} car $f (x) = 5-x - e^{-x}$ avec $\lim_{x \to +\infty} e^{-x} = 0$. \itemalph Pour le calcul de la limite en $-\infty$, l'écriture $f (x) = 5-x - e^{-x}$ donne {\sl a priori\/} une forme indéterminée ($\infty - \infty$) puisque $$ \lim _{x \to -\infty} -x = +\infty \qquad {\rm et} \qquad \lim _{x \to -\infty} -e^{-x} = -\infty $$ On invoque alors le fait que lorsque $x$ tend vers $\pm \infty $, l'exponentielle va plus vite vers sa limite que la fonction polynôme $-x$. On en déduit que \dresultat{\lim_{x \to -\infty} f (x) = -\infty} \itemnum On trouve \dresultat{f' (x) = -1 + e^{-x}}. Et $$ f' (x) \geq 0 \quad \Leftrightarrow \quad e^{-x} \geq 1 \quad \Leftrightarrow \quad \ln \left( e^{-x} \right) \geq \ln (1) \quad \Leftrightarrow \quad -x \geq 0 \quad \Leftrightarrow \quad x \leq 0 $$ d'où le tableau de signe de $f'$ et le tableau de variation de $f$~: $$\dresultat{\vcenter{ \eightpoint\rm \def \hfq{\hfil \ } \offinterlineskip \halign{ % preamble &\hfq #\hfq \cr $x$& \vrule depth 5pt & $-\infty$&& $0$&& $+\infty$% \cr \noalign{\hrule} $f' (x)$& \vrule height 10pt depth 3pt && $+$& $0$& $-$& \cr \noalign{\hrule} \bbuucenter{$f (x)$}& \vrule & \down{$-\infty$}& \bbrightuuparrow & \bbuup{$4$}& \bbrightddownarrow & \down{$-\infty$} \cr }}} $$ \itemalphnum On a $$ \lim_{x \to +\infty} \big( f (x) - (-x+5)\big) = \lim_{x \to +\infty} (-e^{-x}) = 0 $$ donc \tresultat{$D$ asymptote à la courbe $\cal C$ en $+\infty$}. \itemalph \'Etudier la position relative de $\cal C$ et $D$ revient à étudier le signe de la différence $f (x) - (-x+5)$. Comme cette différence est égale à $-e^{-x}$ et que l'exponentielle est toujours strictement positive, on en déduit que cette différence est toujours strictement négative, et donc que \tresultat{$\cal C$ est toujours en dessous de $D$}. \itemalphnum Déterminer les coordonnées du point d'intersection des courbes $\cal C$ et $\Delta$ revient à résoudre le système $$ \cases{ y = f (x) \cr y = -x \cr} \quad \Longleftrightarrow \quad \cases{ -x = 5 - x - e^{-x} \cr y = -x \cr} \quad \Longleftrightarrow \quad \cases{ e^{-x} = 5 \cr y = -x \cr} \quad \Longleftrightarrow \quad \cases{ -x = \ln 5 \cr y = -x \cr} $$ d'où l'unique point d'intersection \mresultat{A (-\ln 5, \ln 5)}. \itemalph Le coefficient directeur de la tangente à la courbe $\cal C$ en $A$ est \mresultat{f' (-\ln 5) = 4}, puisque $f' (-\ln 5) = -1 + e^{\ln 5} = -1+ 5$. \def \epspath{% $HOME/tex_doc/lycee/database/btsmai/analyse/exp/} \epsfxsize = 120mm \itemnum $$ \superboxepsillustrate{etud_001.ps} $$ \itemnum Comme $f (2) = 3 - e^{-2} \approx 2, 86$ est positif, on voit sur le tableau de variation que la fonction $f$ est positive sur l'intervalle $[0, 2]$. L'aire est donc donnée, en unités d'aire, par le calcul de l'intégrale $$ \int_0^2 f (x) \, dx = \int_0^2 5-x - e^{-x} \, dx = \left[ 5x - {x^2 \over2} + e^{-x}\right]_0^2 = 7 + e^{-2}. $$ L'unité d'aire étant de $1\times 1 \cm ^2$, l'aire cherchée est donc $$ \dresultat{{\cal A} = 7 + e^{-2} \cm^2 \approx 714 \mm^2} $$ à $1\mm^2$ près par excès. \fincorrige