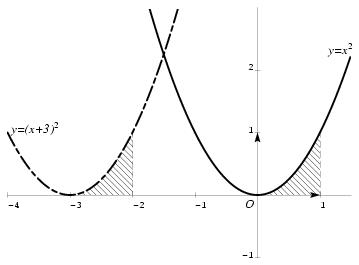
\paragraphe{Intégration par changement de variable} \everymath = {\displaystyle} \sparagraphe{Changement de variable du type $x \mapsto x + \beta$} \exemple{} On se propose de calculer l'intégrale $I = \int_{-3}^{-2} (x+3)^2 \, dx$. On peut faire le calcul directement en remarquant que ${1\over3} (x+3)^3$ est une primitive de $(x+3)^2$ sur $[-3, -2]$. \def \epspath{% $HOME/tex_doc/lycee/database/btsmai/analyse/integr/} \epsfxsize = 70mm \rightsuperboxepsillustrate{cours_06.ps}{-10} On peut également remarquer que, graphiquement, $I$ re\-pré\-sen\-te une mesure de l'aire comprise entre l'axe $0x$ et la courbe $C_1$ d'équation $y=(x+3)^2$ sur l'intervalle $[-3, -2]$. Or cette aire est la même que celle qui est comprise entre l'axe $Ox$ et la courbe $C_2$ d'équation $y=x^2$ sur l'intervalle $[0, 1]$. ($C_2$ est déduite de $C_1$ par une translation de vecteur $3 \vec \imath$.) On en déduit que $$ I = \int_{-3}^{-2} (x+3)^2 \, dx = \int_0^1 x^2 \, dx = \left[ {1\over3} x^3 \right]_0^1 = {1\over3} $$ \finexemple En fait, cet exemple se généralise, et on a le \assert Théorème (admis). Soit $f$ une fonction continue sur un intervalle $I$ du type $I = [a, b+\beta]$ où $a$, $b$ et $\beta \in \rset$ avec $a\leq b$. Alors $$ \dresultat{\int_a^b f (x+\beta) \, dx = \int_{a+\beta}^{b+\beta} f (x) \, dx} $$ \endassert %\exoskip = \bigskip \sparagraphe{Changement de variable du type $x \mapsto \alpha x$ lorsque $\alpha \neq0$} En tenant un raisonnement du même type, mais avec une multiplication de l'échelle sur l'axe des ordonnées, on montre le \assert Théorème (admis). Soit $f$ une fonction continue sur l'intervalle $\alpha a, \alpha b$, où $\alpha \neq 0$. Alors $$ \dresultat{\int_a^b f (\alpha x) \, dx = {1\over\alpha} \int_{\alpha a}^{\alpha b} f (x) \, dx} $$ \endassert \exemple{} On se propose de calculer $I = \int_0^1 e^{2x} \, dx$. On a $ I = \int_0^1 e^{2x} \, dx = {1 \over 2} \int_0^2 e^x \, dx = \left[ e^x \right]_0^2 = {1 \over 2} (e^2 - 1) $ \finexemple