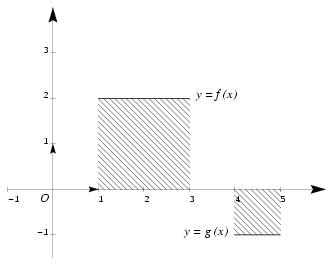
Dans tout ce chapitre, $f$ désigne une fonction continue sur un intervalle $I$ de $\rset$. On désignera par $a$ et $b$ deux nombres fixés quelconques de l'intervalle $I$. \paragraphe {Introduction} Intuitivement, et historiquement, la notion d'{\sl intégrale\/} d'une fonction numérique provient de la notion de calcul d'aire. Le problème à l'origine étant de calculer l'aire d'un domaine plan limité par une courbe. Au fil des siècles, on s'est aperçu que ce problème était exactement l'{\sl inverse\/} du problème qui consistait à chercher la tangente en un point à une courbe donnée. Si je devais donner une définition de l'{\sl intégrale d'une fonction sur un segment\/} à partir de l'approche historique, je donnerais la définition suivante~: \item {} On appelle {\sl intégrale d'une fonction continue $f$ sur le segment $[a, b]$}, et on note $\displaystyle \int _a^b f (x) \, dx$, une mesure {\sl orientée}, en unité d'aire, de l'aire du domaine plan limité par la courbe de la fonction $f$, l'axe $Ox$ et les droites verticales d'équations respectives $x=a$ et $x=b$. \def \epspath {% $HOME/tex_doc/lycee/database/btsmai/analyse/integr/} \epsfxsize = 80mm \item {} Ainsi, si $f$ et $g$ sont les fonctions constantes respectivement définies par $$\displaylines { \eqalign {f : [1, 3] &\rightarrow \rset \cr x &\mapsto 2} \qquad {\rm et} \qquad \eqalign {g : [4, 5] &\rightarrow \rset \cr x &\mapsto -1} \cr \superboxepsillustrate {cours_12.ps} \cr {\rm Alors} \qquad \int _1^3 f (x) \, dx = 4 \qquad {\rm et} \qquad \int _4^5 g (x) \, dx = -1 \cr }$$ Malheureusement, cette définition nous emmènerait dans des méandres calculatoires complexes pour montrer comment on peut calculer une intégrale donnée. Aussi nous partirons de la définition abstraite de l'intégrale à partir des primitives d'une fonction.