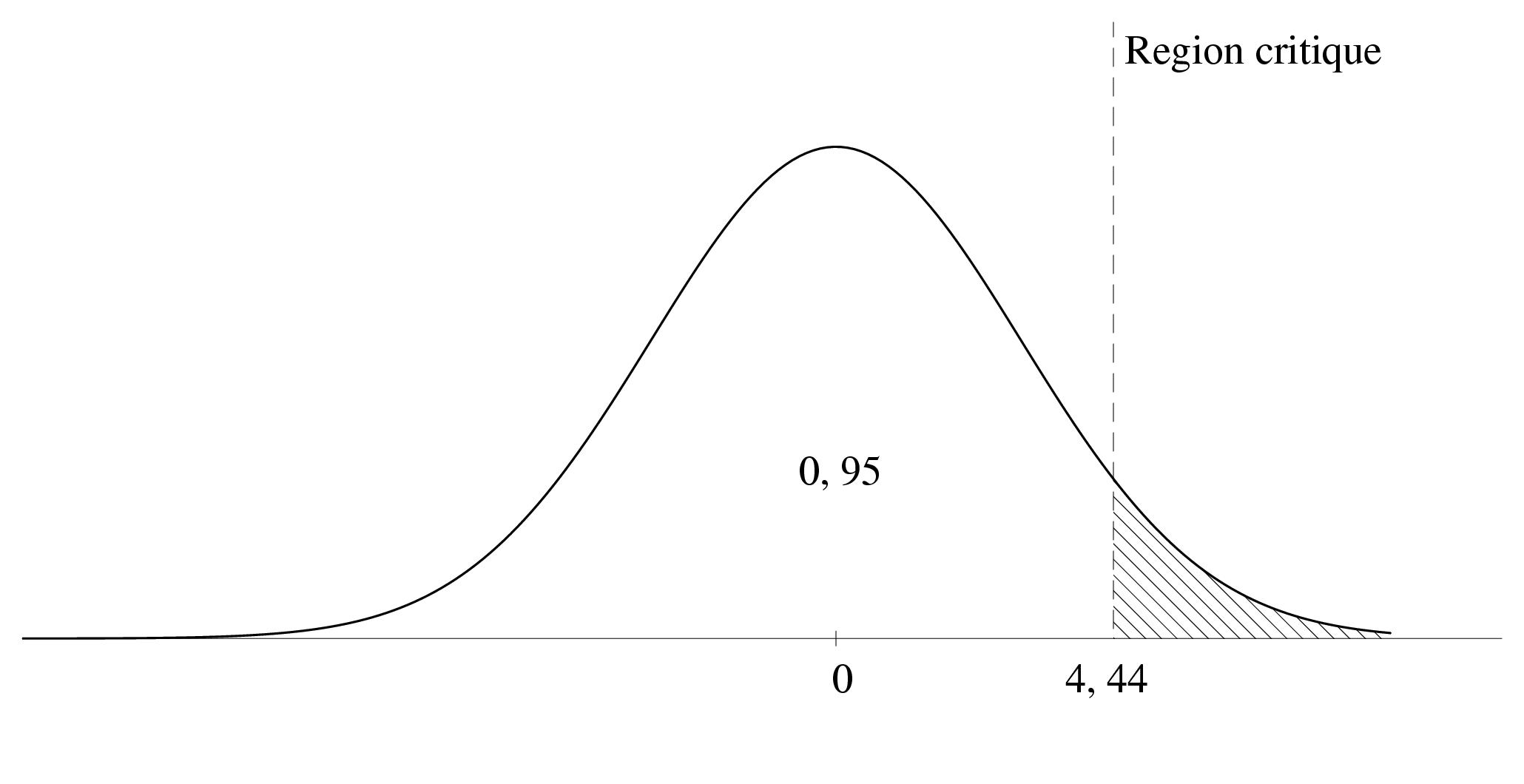
\paragraphe{Un dernier exemple} \sparagraphe{Définition du problème} Toujours avec les donnéees précédentes, comment construire et utiliser un test permettant de décider, à partir des mêmes échantillons, si la moyenne des masses des pièces livrées par le fournisseur $B$ est significativement supérieure, au seuil de $5\%$, à celle du fournisseur $A$~? \sparagraphe{Construction du test unilatéral} \item{$\bullet$} {\sl Choix de $H_0$~:} $m_A = m_B$. \item{} {\sl Choix de $H_1$~:} $m_A > m_B$. \item{$\bullet$} {\sl détermination de la région critique au seuil de $5\%$} \item{} Sous l'hypothèse $H_0$, $D$ suit la loi normale ${\cal N} (0\, ; 2, 7)$, donc $D/2, 7$ suit la loi normale centrée réduite ${\cal N} (0, 1)$. En particulier, on a $p (D/2, 7 \leq t) = 0, 95$ lorsque $t = 1, 645$ (par lecture du formulaire), et donc $p (D < 4, 44) = 0, 95$. \def \epspath{% $HOME/tex_doc/lycee/database//btsmai/stats/infer/} \epsfxsize 100mm $$ \epsillustrate{cour_008.ps} $$ \item{$\bullet$} {\sl \'Enoncé de la règle de décision} \item{} On prélève avec remise un échantillon aléatoire de taille $n_A = 30$ de la population $A$ et on calcule sa moyenne $\bar x_A$; on fait de même pour la population $B$ avec $n_B = 50$. On pose $d = \bar x_B - \bar x_A$. \itemitem{} si $d \leq 4, 44$ on accepte $H_0$. \itemitem{} si $d > 4, 44$ on rejette $H_0$ et on accepte $H_1$. \sparagraphe{Utilisation du test unilatéral} \item{$\bullet$} {\sl Calcul de $d$} \item{} On a $d = \bar x_B - \bar x_A = 779, 6 - 774, 7 = 4, 9$ \item{$\bullet$} {\sl Application de la règle de décision} \item{} Comme $4, 9 > 4, 44$, on rejette $H_0$ et on accepte $H_1$. Au seuil de $5\%$, la moyenne des masses des pièces livrées par le fournisseur $B$ est significativement supérieure à celle du fournisseur $A$.