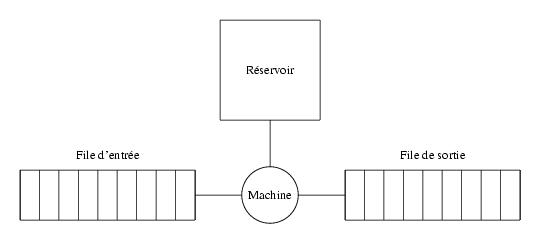
\exo {Une chaîne d'embouteillage, {\sl bts mai, mai 2003}} \centerline {\bf Les quatres questions de cet exercice sont indépendantes} \epsfxsize 79.9mm \def \epspath {% $HOME/tex_doc/lycee/database/btsmai/stats/infer/} \rightepsillustrate {synt_007.ps} {-10} % Dans une usine du secteur de l'a\-gro\-ali\-men\-tai\-re, une machine à em\-bou\-teil\-ler est alimentée par un réservoir d'eau et par une file d'ap\-pro\-vi\-sion\-ne\-ment en bouteilles vides, selon le schéma ci-contre. L'exercice consiste en une étude sta\-tis\-ti\-que du bon fonctionnement de ce système. \itemnum {\sl Défaut d'approvisionnement} \item {} On considère qu'il y a défaut d'approvisionnement~: \itemitem {--} soit lorsque la file d'entrée des bouteilles est vide, \itemitem {--} soit lorsque le réservoir est vide. \item {} On tire au hasard un jour ouvrable dans une année. On note $A$ l'événement ~: \og \sl la file d'attente est vide au moins une fois dans la journée\fg \ et $B$ l'événement~: \og \sl le réservoir est vide au moins une fois dans la journée\fg. \item {} On suppose que les événements $A$ et $B$ sont indépendants et une étude statistique a montré que $$ p (A) = 0, 04 \qquad {\rm et} \qquad p (B) = 0, 02. $$ \item {} Calculer la probabilité des événements suivants~: \itemitemalph $E_1 = A\cap B$. \itemitemalph $E_2$~: \og \sl la machine a connu au moins un défaut d'approvisionnement dans la journée\fg . \itemnum {\sl Pannes de la machine sur une durée de 100 jours} \item {} On note $X$ la variable aléatoire qui à toute période de 100 jours consécutifs, tirée au hasard dans les jours ouvrables d'une année, associe le nombre de pannes de la machine. Une étude, menée par le constructeur sur un grand nombre de machines de ce type, permet d'admettre que $X$ suit la loi de Poisson de paramètre $\lambda = 0, 5$. \item {} Déterminer, à l'aide de la table du formulaire~: \itemitemalph $p (X\leq 2)$; \itemitemalph la probabilité de l'événement \og \sl la machine a au plus quatre pannes pendant la période de 100 jours consécutifs\fg ; \itemitemalph le plus petit entier $n$ tel que~: $p (X \leq n)\geq 0, 99$. {\bf Dans tout ce qui suit, les volumes sont exprimés en litres et tous les résultats approchés sont à arrondir à $\bf 10^{-3}$}. \itemnum {\sl Qualité de l'embouteillage à la sortie} \item {} On désigne par $Y$ la variable aléatoire qui, à toute bouteille prise au hasard dans la production d'une heure, associe le volume d'eau qu'elle contient. On admet que, lorsque la machine est bien réglée, $Y$ suit la loi normale de moyenne $1, 5$ et d'écart-type $0, 01$. \item {} Une bouteille d'eau est conforme aux normes de l'entreprise lorsqu'elle contient entre $1, 47$ et $1, 53$ litre d'eau. \item {} Calculer la probabilité qu'une bouteille satisfasse à la norme. \itemnum {\sl Fiabilité d'une machine à embouteiller} \item {} On s'intéresse à une machine à embouteiller prélevée au hasard dans le parc des machines sur le point d'être livrées par le constructeur. \item {} On désigne par $T$ la variable aléatoire qui, à toute machine prélevée au hasard dans le parc, asssocie sa durée de vie avant une défaillance. \item {} On note $p (T>t)$ la probabilité qu'une machine prélevée au hasard dans le parc n'ait pas de défaillance avant l'instant $t$, exprimé en jours. \item {} On suppose que $p (T>t) = e^{-0, 005t}$. \itemitemalph Calculer la probabilité qu'une machine prélevée au hasard dans le parc fonctionne plus de 200 jours sans panne. \itemitemalph Déterminer $t$ pour que la probabilité qu'une machine prélevée au hasard dans le parc fonctionne plus de $t$ jours, soit égale à $0, 8$. Arrondir à l'entier par défaut. \finexo \corrige \itemalphnum Les événements $A$ et $B$ étant indépendants, il vient $$ p (E_1) = p (A\cap B) = p (A) \times p (B) = 0, 04\times 0, 02 \qquad {\rm soit} \qquad \dresultat {p (E_1) = 8 \cdot 10^{-4}} $$ \itemalph Il vient $$ p (E_2) = p (A\cup B) = p (A) + p (B) - p (A\cap B) = 0, 04 + 0, 02 - 8 \cdot 10^{-4} \qquad {\rm soit} \qquad \dresultat {p (E_2) = 0, 0592} $$ \itemnum \` A l'aide du formulaire, il vient $$\eqalign { p (X\leq 2) &= p (X=0) + p (X=1) + p (X=2) \cr &= 0, 606\, 5 + 0, 303\, 3 + 0, 075\, 8 \qquad {\rm soit} \qquad \dresultat {p (X\leq 2) = 0, 985\, 6} }$$ \itemalph Répondre à la question revient à déterminer $p (X\leq 4)$. Il vient alors $$ p (X\leq 4) = p (X\leq 2) + p (X= 3) + p (X=4) \qquad {\rm soit} \qquad \dresultat {p (X\leq 4) = 0, 999\, 8} $$ \itemalph Et comme le calcul de $p (X\leq 3)$ nous donne $p (X\leq 3) = 0, 998\, 2$, l'entier cherché est \dresultat {n = 3}. \itemnum Si la variable $Y$ suit la loi normale ${\cal N} (1, 5 ; 0, 01)$, alors la variable $T = (Y - 1, 5)/0, 01$ suit la loi normale ${\cal N} (0 ; 1)$. Il vient alors~: $$\eqalign { p (1, 47\leq Y \leq 1, 53) &= p \left( {-0, 03\over 0, 01}\leq {Y - 1, 5\over 0, 01}\leq {0, 03\over 0, 01}\right) \cr &= p (-3\leq T\leq 3) = 2\Pi (3) - 1 \qquad {\rm soit} \qquad \dresultat {p (1, 47\leq Y \leq 1, 53) = 0, 997\, 3\approx 0, 997} \cr }$$ \itemalphnum On a immédiatement $$ p (T > 200) = e^{-0, 005 \times 200} = e^{-1} \qquad {\rm soit} \qquad \dresultat {p (T > 200) \approx 0, 368} $$ \itemalph Et comme $p (T > t) = e^{-0, 005t}$, la relation $p (T>t) = 0, 8$ entraîne $$ e^{-0, 005t} = 0, 8 \quad \Longrightarrow \quad -0, 005 t = \ln 0, 8 \quad \Longrightarrow \quad t = {-\ln 0, 8\over 0, 005}\approx 44, 63. $$ La valeur cherchée est donc \tresultat {$t = 44$ jours}. \fincorrige