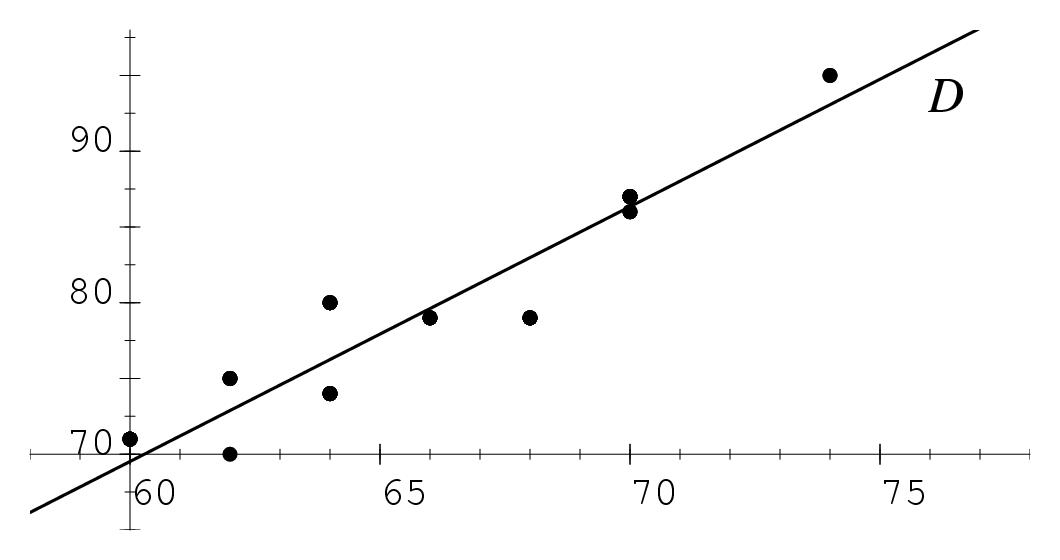
\exo{Méthode des moindres carrés~: charge de rupture d'un acier} Le tableau suivant donne les résultats obtenus à partir de 10~essais de laboratoire concernant la charge de rupture d'un en fonction de sa teneur en carbone.\par \centerline { \vbox{\halign{ \offinterlineskip %% preamble #\tv && \cc{#}& #\tv \cr \noalign{\hrule} & Teneur en carbone $x_i$&& 70&& 60&& 68&& 64&& 66&& 64&& 62&& 70&& 74&& 62& \cr \noalign{\hrule} & Charge de rupture $y_i$ (en kg)&& 87&& 71&& 79&& 74&& 79&& 80&& 75&& 86&& 95&& 70& \cr \noalign{\hrule} }}} \itemnum Représenter graphiquement le nuage de points $(x_i, y_i)$. On prendra 1~cm (ou 1~grand carreau) en abscisse pour une unité, en représentant les abscisses à partir de la valeur 60. En ordonnée, on prendra 1~cm (ou 1~grand carreau) pour 2~kg, en représentant les ordonnées à partir de 70. \itemnum Calculer les coordonnées du point moyen de ce nuage. \itemnum Déterminer la valeur approchée à $10^{-3}$ près du coefficient de corrélation linéaire de la série statistique de variables $x$ et $y$. Interpréter le résultat. \itemitemalphnum Déterminer une équation de la forme $y = ax+b$ de la droite $D$ de régression de $y$ en $x$ par la méthode des moindres carrés. On donnera des valeurs approchées des coefficients $a$ et $b$ à $10^{-3}$ près. \itemitemalph Tracer la droite $D$ sur le graphique. \itemnum Un acier a une teneur en carbone de $77$. Donner une estimation de sa charge de rupture. \finexo \corrige{} \def \epspath{% $HOME/tex_doc/lycee/database/btsmai/stats/} \epsfxsize = 80mm \itemnum $$ \superboxepsillustrate{reg_004.ps} $$ \itemnum Pour le point moyen, on calcule la moyenne arithmétique de chacun des caractères. On trouve ainsi $$ \dresultat{G~: \left( 66; {398 \over5} \right)} \qquad {\rm soit} \qquad \dresultat{G~: ( 66; 79,6)} $$ \itemnum %% On trouve successivement %% $$ %% \bar x = 66, %% \qquad %% \sigma (x) = {2\over5} \sqrt{110} \simeq 4,195\ ; %% \qquad {\rm et} \qquad %% \bar y = 79,6\ ; %% \qquad %% \sigma (y) = {1\over5} \sqrt{1381} \simeq 7,432 %% $$ %% Le calcul de la covariance et du coefficient de corrélation linéaire %% par les formules %% $$ %% \sigma_{xy} = {1\over n} \left( \sum_{i=1}^n x_iy_i\right) - \bar %% x\bar y, %% \qquad {\rm et} \qquad %% r = {\sigma_{xy} \over \sigma (x) \times \sigma (y)} %% $$ %% donne alors %% $$ %% \dresultat{\sigma_{xy} = {148 \over5} = 29,6} %% \qquad {\rm et} \qquad %% \dresultat{r \simeq 0,949} %% $$ \`A la calculatrice, on trouve \dresultat{r \simeq 0,949}. Le coefficient de corrélation étant plutôt \og bon\fg\ (ie \og proche\fg\ de~1), une approximation affine paraît adaptée. \itemnum %% La droite $D$ de régression de $y$ en $x$ possède une %% équation de la forme $y = ax+b$, où $a$ et $b$ vérifient %% $$ %% a = {\sigma_{xy} \over [\sigma (x)]^2}, %% \quad {\rm soit} \quad %% \dresultat{a = {37 \over 22} \simeq 1,682} %% \qquad {\rm et} \qquad %% \bar y = a \bar x + b, %% \quad {\rm soit} \quad %% \dresultat{b = -{157 \over5} = -31,4} %% $$ La droite $D$ de régression de $y$ en $x$ possède une équation de la forme $y = ax+b$. Toujours à la calculatrice, on trouve l'équation cherchée~: \mresultat{D: y = 1,682 x -31,4} \itemnum En utilisant cette droite de régression, on trouve alors pour une teneur en carbone de $x = 77$, une charge de rupture de \mresultat{y \simeq 98, 114 \kg}. \fincorrige